데이터 집합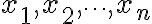 
의 표본평균,sample_mean과 표본표준편차,sample_standard_deviation를 
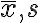라고 하자 ( 
). 
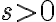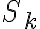를 다음과 같이 정의한다.
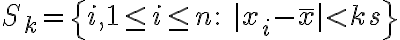
이 경우 임의의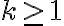 
에 대해 다음이 성립한다.
}{n}\ge 1-\frac{n-1}{nk^2} > 1-\frac1{k^2} "$\frac{N(S_k)}{n}\ge 1-\frac{n-1}{nk^2} > 1-\frac1{k^2}$")
(mimeTeX에서 분모 n이 너무 작게 표시되어서 다시)
%7D%7Bn%7D%5Cge%201-%5Cfrac%7Bn-1%7D%7Bnk%5E2%7D%20%3E%201-%5Cfrac1%7Bk%5E2%7D)
N(): 집합 원소의 개수
(Ross p.29)
tmp from http://blog.naver.com/mykepzzang/220838855204 중간
확률변수 X가 평균 "$(\mu)$")
으로부터 표준편차  "$(\sigma)$")
의 c배 범위 내의 값을 취할 확률은 적어도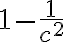 
이다. 즉,
 \ge 1-\frac{1}{c^2} "${\rm P}(\mu-c\sigma < X < \mu+c\sigma) \ge 1-\frac{1}{c^2}$")
이다.
확률변수 X가 평균
tmp from ![[https]](http://tomoyo.ivyro.net/123/imgs/https.png)
namuwiki(https://namu.wiki/w/%EC%B2%B4%EB%B9%84%EC%87%BC%ED%94%84%20%EB%B6%80%EB%93%B1%EC%8B%9D)
확률분포,probability_distribution를 정확히 모를 때 해당 확률분포의 평균과 표준편차의 값만으로 특정한 확률의 최솟값만큼은 알아낼 수 있는 부등식.
ex. 확률변수 X가 (~ 범위) 내에 있을 확률은 확률분포에 관계없이 적어도 (~) 이상
namuwiki(https://namu.wiki/w/%EC%B2%B4%EB%B9%84%EC%87%BC%ED%94%84%20%EB%B6%80%EB%93%B1%EC%8B%9D)확률분포,probability_distribution를 정확히 모를 때 해당 확률분포의 평균과 표준편차의 값만으로 특정한 확률의 최솟값만큼은 알아낼 수 있는 부등식.
ex. 확률변수 X가 (~ 범위) 내에 있을 확률은 확률분포에 관계없이 적어도 (~) 이상
마르코프_부등식,Markov_inequality은 이것을 증명하는 데 도움을 줌
tmp 참고 bookmarks
ko
https://m.blog.naver.com/hafs_snu/220831180799
https://bluehorn07.github.io/mathematics/2021/03/17/chebyshev%27s-inequality.html
체비쇼프 부등식
ko
https://m.blog.naver.com/hafs_snu/220831180799
https://bluehorn07.github.io/mathematics/2021/03/17/chebyshev%27s-inequality.html체비쇼프 부등식Chebyshev’s inequality
AKA 체비쇼프 부등식
AKA 체비쇼프 부등식
Up: 부등식,inequality