초기값 문제, initial value problem, IVP
미분방정식 =0) 의 일반해,general_solution는 임의의 상수를 포함하고 있는데, 어떤 특정한 점
의 일반해,general_solution는 임의의 상수를 포함하고 있는데, 어떤 특정한 점 ) 을 지나는 해를 알고 싶다면, 이 점을 지나는 특정한 적분곡선을 찾아야 한다. 이것을 초기값 문제(initial value problem)라고 하며,
을 지나는 해를 알고 싶다면, 이 점을 지나는 특정한 적분곡선을 찾아야 한다. 이것을 초기값 문제(initial value problem)라고 하며, 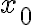 와
와 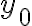 에 대해서 1계 초기값 문제는
에 대해서 1계 초기값 문제는
=0;\;\; y(x_0)=y_0)
으로 나타낼 수 있다. 이 때 조건
=y_0)
을 초기조건,initial_condition이라고 한다.
(O'Neil p4)
일반해,general_solution에는 적분상수가
(한광희)
1st order IVP
Solve
,) subjected to
subjected to
=y_0)
2nd order IVP
Solve
,) subjected to
subjected to
=y_0) and
and
=y_1)
nth order IVP
} \right),) subjected to
subjected to
=y_0)
=y_1)

}(x_0)=y_{n-1})
(Beelee)
Solve
Solve
REL.
Cauchy_problem or Cauchy_initial_value_problem - Cauchy_IVP (writing)
Cauchy_problem or Cauchy_initial_value_problem - Cauchy_IVP (writing)
Compare: 경계값문제,boundary_value_problem,BVP
{
미분방정식,differential_equation with 경계조건
문제,problem
boundary_value =,boundary_value . { boundary_value }
boundary_value }
 Boundary_value_problem = https://en.wikipedia.org/wiki/Boundary_value_problem
Boundary_value_problem = https://en.wikipedia.org/wiki/Boundary_value_problem
 경계값_문제
경계값_문제
{
미분방정식,differential_equation with 경계조건
문제,problem
boundary_value =,boundary_value . {
}
https://mathworld.wolfram.com/InitialValueProblem.html
 초기값_문제
초기값_문제
 Initial_value_problem
Initial_value_problem
https://planetmath.org/initialvalueproblem
http://www.scholarpedia.org/article/Initial_value_problems
https://planetmath.org/initialvalueproblem
http://www.scholarpedia.org/article/Initial_value_problems
----

