양수항과 음수항이 번갈아 나타나는 무한급수,infinite_series.

급수,series가 양수항과 음수항을 교대적으로 가질 때, 이러한 급수를 교대급수(alternating series)라고 한다.[1]

이것의 각 항,term이
$a_n=(-1)^n|a_n|$
or
$a_n=(-1)^{n-1}|a_n|$ ///// 원래있던내용. 뭐보고 썼더라

그래서 교대급수,alternating_series는 //// wpen
$\sum_{n=0}^{\infty}(-1)^n a_n$
or
$\sum_{n=0}^{\infty}(-1)^{n+1}a_n$
with $\forall n, a_n > 0.$

See also 교대급수판정법,alternating_series_test

교대조화급수 alternating harmonic series
{
$1-\frac12+\frac13-\frac14+\frac15-\cdots+\frac{(-1)^{n+1}}{n}+\cdots$
이 급수는 수렴한다.
(Thomas)

$\sum_{n=1}^{\infty}(-1)^{n+1}\frac1n = 1-\frac12+\frac13-\frac14+\cdots=\ln 2$ 라는데 chk

ALSOIN, MERGE: 조화급수,harmonic_series#s-2
}

정리 (교대급수의 어림 정리)

$S=\sum_{n=1}^{\infty}(-1)^{n-1}b_n\;\;(b_n>0)$ 은 다음 조건을 만족하는 교대급수의 합이라 하자.

$1.\; b_{n+1}\le b_n\;(n=1,2,3,\ldots)$
$2.\; \lim_{n\to\infty}b_n = 0$

그러면 $S_n=\sum_{k=1}^{n} (-1)^{k-1} b_k$ 라 할 때
$\left|S-S_n\right| \le b_{n+1}$ 이다.


교대급수 정리
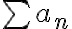교대급수 $\textstyle\sum a_n$ 은 수렴한다.

라이프니츠가 발견.

(김홍종 미적분학 1+ p37)

$1-\frac13+\frac15-\frac17+\frac19-\cdots=\frac{\pi}{4}$

Twins:
[https]수학백과: 교대급수(https://terms.naver.com/entry.naver?docId=3404968&cid=47324&categoryId=47324)
WpKo:교대급수
WpEn:Alternating_series
https://everything2.com/title/Alternating series

https://encyclopediaofmath.org/wiki/Alternating_series
https://mathworld.wolfram.com/AlternatingSeries.html

Related:
부호,sign

Up: 급수,series > 무한급수,infinite_series
alternation
----
Retrieved from http://tomoyo.ivyro.net/123/wiki.php/교대급수,alternating_series
last modified 2023-12-12 03:13:22