(Stewart)
급수
^{n+1} u_n = u_1 - u_2 + u_3 - u_4 + \cdots)
이 다음의 세 가지 조건을 만족시키면 수렴한다.
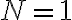 이라고 하자.
이라고 하자.  이 짝수인 정수, 즉
이 짝수인 정수, 즉 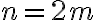 이면 처음
이면 처음  항의 합은 다음과 같다.
항의 합은 다음과 같다.
+(u_3-u_4)+\cdots+(u_{2m-1}-u_{2m}))
-(u_4-u_5)-\cdots-(u_{2m-2}-u_{2m-1})-u_{2m})
첫 번째 줄 식에서 괄호 안 각 항이 0 또는 양수이므로,
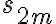 은 음이 아닌 항들의 합임을 알 수 있다.
은 음이 아닌 항들의 합임을 알 수 있다.
따라서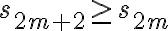 이고
이고 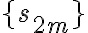 은 감소하지 않는 수열이다.
은 감소하지 않는 수열이다.
두 번째 줄 식에서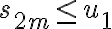 임을 알 수 있다.
임을 알 수 있다. 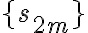 은 감소하지 않는 수열이고 위로 유계,bounded이므로 다음의 극한값을 가진다.
은 감소하지 않는 수열이고 위로 유계,bounded이므로 다음의 극한값을 가진다.
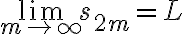
 이 홀수인 정수, 즉
이 홀수인 정수, 즉  이면, 처음
이면, 처음  항의 합은
항의 합은 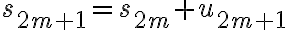 이다.
이다. 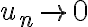 이므로
이므로
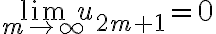
이고, 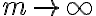 임에 따라
임에 따라
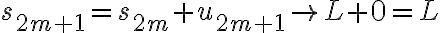
이다. 위 두 극한 식을 결합하면 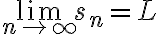
(Thomas 13e ko 8.6 p494 정리15 교대급수판정법)
- 모든
에 대해
- 적당한 정수
이 존재하여 모든
에 대해,
즉 양수
은 결국 감소한다.
따라서
두 번째 줄 식에서
(Thomas 13e ko 8.6 p494 정리15 교대급수판정법)
If
^{n-1}b_n=b_1-b_2+b_3-b_4+\cdots\;\;(b_n>0))
satisfies
(i) 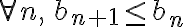
(ii)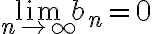
then the alternating series is convergent.(ii)
pf.
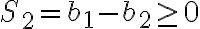
\ge S_2)
\ge S_{n-2})
⇒ {S2n} is increasing and
-(b_4-b_5)-\cdots\le b_1)
...
⇒ {S2n} is increasing and
(괄호 안의 값은 0이상인데 이것을 계속 빼주니까)
⇒ {S2n} is bounded aboveby M.S.T.(monotonic sequence theorem), {S2n} converges.
That is, (짝수인 경우 증명)
(짝수인 경우 증명)
That is,
Also =S+0=S)
therefore,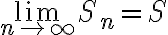
hence^{n-1}b_n) is convergent.
is convergent.
(이부분 비디오가 흐려서 CHK)
therefore,
hence
(이부분 비디오가 흐려서 CHK)
이 문단 from http://www.kocw.net/home/cview.do?cid=293242 11.5 교대급수


![[https]](/123/imgs/https.png)