가역행렬,invertible_matrix

정사각행렬,square_matrix 중에서 행렬의 곱셈(행렬곱셈,matrix_multiplication)에 대한 역원,inverse_element이 존재하는 행렬.

n차 정사각행렬 A와 n차 단위행렬 In에 대해
$AB=I_n=BA$
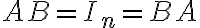
를 만족하는 n차 정사각행렬 B가 존재하면 A를 가역행렬이라 한다.
이 때 식을 만족하는 B는 하나뿐이며 이것을 A의 역행렬,inverse_matrix이라 한다.

//바로 위 문단 다시썼는데 chk
{
n차 정사각행렬 A와 n차 단위행렬 In에 대해
$AB=I_n=BA$
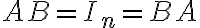
를 만족하는 n차 정사각행렬 B가 존재하면:
A를 가역행렬(invertible, nonsingular)이라 한다.
이 때 식을 만족하는 B는 하나뿐이며 이것을 A의 역행렬,inverse_matrix이라 한다.
이러한 B가 존재하지 않으면:
A는 비가역(noninvertible, singular)이라 한다.
}


가역행렬은 행렬식,determinant의 값이 0이 아니다.
TBW proof

가역행렬 = invertible matrix = 비특이행렬 = nonsingular matrix = 정칙행렬 = regular matrix
비가역행렬 = noninvertible matrix = 특이행렬 = singular matrix (특이행렬,singular_matrix)
역행렬 = inverse matrix



[edit]

1. again..

정방행렬(정사각행렬,square_matrix) A에 대해 다음 식
AB=I=BA
를 만족하는 B가 존재하면,
A : 가역행렬 invertible matrix = 비특이행렬 nonsingular matrix
B : 역행렬,inverse_matrix, A−1로 표기
만약 B가 존재하지 않으면, 그러한 A를 부르는 이름은
A : 비가역행렬 non-invertible matrix = 특이행렬 singular matrix
(KU정태수)

비가역행렬,noninvertible_matrix A와 방정식 Ax=b 에 대해.

A가 non-invertible하면, Ax=b will have either no solution or infinitely many solutions.
(주재걸)

[edit]

2. 용어, 같은 것

[edit]

3. 성질

A가 가역행렬이면, A-1은 가역행렬이며
(A-1)-1=A이다.
A와 B가 정사각 가역행렬이면, AB도 그렇고, 그 역행렬은
(AB)-1=B-1A-1이다.
A가 가역행렬이면, AT도 그렇고, 그 역행렬은
(AT)-1=(A-1)T이다.

(Lay, 2.2 The Inverse of a Matrix, Thm 6)
행렬 A가 가역이면
1. A-1은 유일하다.
2. (A-1)-1=A
3. (kA)-1=(1/k)A-1
4. An도 가역이며, (An)-1=(A-1)n 이다.
(n=0, 1, 2, ...)
5. AT도 가역이며, (AT)-1=(A-1)T 이다.

가역이라는 것과 필요충분조건인(동치인) 조건이 많은데, 정리할것, TBW
참고 https://blog.naver.com/ptm0228/221685537743
모든 실수 가역행렬 A에 대해 두 행렬의 곱 ATA는 양의정부호행렬,positive_definite_matrix.
Source: WpEn:Definite_matrix 에서 "For any real invertible matrix"

[edit]

4. 나카이 에츠지

(정칙행렬=가역행렬. 정칙행렬은 일본어인가?)
역행렬이 존재하는 행렬 : 정칙행렬

A와 B가 모두 정칙이면
AB도 정칙이고, 그 역행렬은
(AB)-1=B-1A-1

[edit]

5. 가역행렬과 행렬식

행렬식,determinant과 가역행렬 사이의 관계

다음은 같은 뜻.
  • $A$ 가 가역행렬
  • $\det(A)\ne 0$

see https://wikidocs.net/76267 3. 행렬식과 가역행렬

AKA 정칙행렬(regular matrix) - 정칙행렬,regular_matrix