기호 : 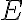
단위행렬에 기본행연산 한 번을 수행해 얻어진 행렬.
단위행렬,unit_matrix에 기본행연산,elementary_row_operation,ERO을 한 번 해서 얻을 수 있는 행렬.
단위행렬,unit_matrix에 기본행연산,elementary_row_operation,ERO을 한 번 적용해서 얻은 행렬.
단위행렬,unit_matrix에 기본행연산,elementary_row_operation,ERO을 한 번 해서 얻을 수 있는 행렬.
단위행렬,unit_matrix에 기본행연산,elementary_row_operation,ERO을 한 번 적용해서 얻은 행렬.
Identity matrix(단위행렬,unit_matrix)과 ERO(기본 행 연산) 한 번의 차이가 있음.
단위행렬도 기본행렬의 한 종류. (단위행렬에 상수 1을 1행에 곱하는 기본행연산을 해도 단위행렬이므로)
임의의 정사각행렬,square_matrix을 아래삼각행렬(lower triangular matrix)과 위삼각행렬(upper triangular matrix)의 곱으로 표현하는 데, 즉 LU분해,LU_decomposition하는 데 사용.
성질 (checkout https://wikidocs.net/75492)
* 기본 행렬의 역행렬은 기본 행렬이다.
* 임의의 행렬의 왼쪽에 기본행렬을 곱한 결과(EA=...)는 기본행렬에 대응하는 기본행 연산을 주어진 임의의 행렬에 시행한 결과와 같다.
* 기본 행렬의 역행렬은 기본 행렬이다.
* 임의의 행렬의 왼쪽에 기본행렬을 곱한 결과(EA=...)는 기본행렬에 대응하는 기본행 연산을 주어진 임의의 행렬에 시행한 결과와 같다.
ex.
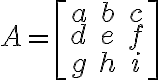
일 때
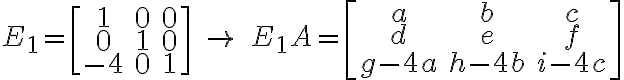
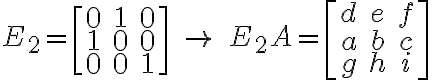
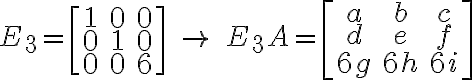
그리고 치환행렬,permutation_matrix은
(BigBook)
Up: 행렬,matrix


![[https]](/123/imgs/https.png)