Difference between r1.19 and the current
@@ -8,6 +8,8 @@
ALSOIN [[샘플링,sampling]]= 비교 =
[[순서,order]] 여부와 와 중복가능('with replacement'?)여부로 4가지 경우.
|| || 중복 불허 || 중복 허용 ||
|| 순서 중요 ([[수열,sequence]]처럼 ... '일렬로 배열'|| ||중복순열 ${}_n\mathrm{\Pi}_{r}=n^r$ ||
@@ -21,6 +23,11 @@
||배열 순서 고려 ||$n^k$ ||$\frac{n!}{(n-k)!}$ ||||배열 순서 무시 ||$\binom{n+k-1}{k}$ ||$\binom{n}{k}$ ||
from http://www.kocw.net/home/search/kemView.do?kemId=1052562
|| ||order unimportant ||order important ||
||without[[br]]replacement ||$\binom{n}{k}=\frac{n(n-1)\cdots(n-k+1)}{k!}$ ||$n(n-1)(n-2)\cdots(n-k+1)$ ||
||with[[br]]replacement ||$\binom{n+k-1}{k}=\frac{(n+k-1)!}{(n-1)!k!}$ ||$n^k$ ||
from http://rosettacode.org/wiki/Permutations 앞 .....CHKCHK
----
ISO 80000-2에 따른 기호는
@@ -48,5 +55,4 @@
----
Up: [[경우의_수]] 혹은 [[조합론,combinatorics]]
비교 ¶
순서,order 여부와 와 중복가능('with replacement'?)여부로 4가지 경우.
서로 다른  개에서
개에서  개를 택하는 경우의 수를 가정- 중복순열+중복조합 설명에 ok, 나머지 2가지의 경우 모두 chk
개를 택하는 경우의 수를 가정- 중복순열+중복조합 설명에 ok, 나머지 2가지의 경우 모두 chk
계산법은
from http://www.kocw.net/home/search/kemView.do?kemId=1052562
| 중복 불허 | 중복 허용 | |
| 순서 중요 (수열,sequence처럼 ... '일렬로 배열' | 중복순열 | |
| 순서 무관 (집합,set처럼 | 중복조합 |
| 복원 추출 | 비복원 추출 | |
| 배열 순서 고려 | 순열,permutation | |
| 배열 순서 무시 | 조합,combination |
| 복원 추출 | 비복원 추출 | |
| 배열 순서 고려 | ||
| 배열 순서 무시 |
| order unimportant | order important | |
| without replacement | ||
| with replacement |
ISO 80000-2에 따른 기호는
그 값은
The term "permutation" is used when 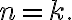
from https://people.engr.ncsu.edu/jwilson/files/mathsigns.pdf#page=20
| number of … | with repetition | without repetition |
| combinations | ||
| variations |
| number of … | with repetition | without repetition |
| combinations | ||
| variations |
from https://people.engr.ncsu.edu/jwilson/files/mathsigns.pdf#page=20
프로그래밍 언어 구현 (계산 소스) ¶
from https://wikidocs.net/23278 CHK
{
Python에서는 import itertools 후에
}
{
Python에서는 import itertools 후에
| 순열 | |
| 중복순열 | |
| 조합 | |
| 중복조합 |

