정의:
n차 정사각행렬 A에 대해, 다음을 만족하는 B가 있으면 A는 가역(invertible)이다.
표기:AB=In=BA
이 때 B를 A의 역행렬(inverse matrix)이라 하며, 이러한 B가 없으면 A는 비가역(noninvertible)이다.A의 역행렬 = A−1
따라서 AA−1=A−1A=IA는 det(A)≠0일 때에만 역행렬을 가진다.
역행렬이 존재한다면 유일하다(unique). // 유일성,uniqueness
행렬의 곱셈에 대한 역원,inverse_element.
1. TMP CHK ¶
용어가 난립하고 혼란스러워서 대대적 정리 및 비교표 필요 ex. singular/nonsingular/정칙/비정칙/가역/비가역/invertible/inverse/....
{
invertible matrix = nonsingular matrix
AB=BA=I
여기서 A, B는 둘 다 invertible(=nonsingular) 행렬에 속함.
그리고 A, B는 서로 inverse matrix임.
여기서 A, B는 둘 다 invertible(=nonsingular) 행렬에 속함.
그리고 A, B는 서로 inverse matrix임.
A는 있는데 위 식을 만족하는 B가 존재하지 않으면, A는 singular matrix에 속함.
nonsingular matrix의 inverse matrix는 유일함. i.e.
nonsingular matrix는 단 하나의 inverse matrix를 가짐. (아래 밑에 증명까지 적어놓은 게 있네.)
nonsingular matrix는 단 하나의 inverse matrix를 가짐. (아래 밑에 증명까지 적어놓은 게 있네.)
역행렬의 조건:
A가 nonsingular matrix일 필요충분조건은 A의 determinant가 0이 아니라는 것. i.e.
det(A)≠0
A가 nonsingular matrix일 필요충분조건은 A의 determinant가 0이 아니라는 것. i.e.
det(A)≠0
| 역행렬을 갖는 경우 | 정칙행렬,regular_matrix | nonsingular matrix |
| 역행렬을 갖지 않는 경우 | 특이행렬,singular_matrix | singular matrix |
A가 n×n행렬일 때
| rank(A)=n | A는 정칙행렬 | det(A)≠0 | |
| rank(A)<n | A는 특이행렬 | 그럼여기는 det(A)=0? CHK |
2. 2×2 행렬의 역행렬 ¶
Let
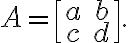
If det(A)=ad−bc=0 : A is not invertible.
If det(A)=ad−bc≠0 : A is invertible and
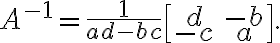
If det(A)=ad−bc≠0 : A is invertible and
4.1. 1. ¶
n차의 정사각행렬 A가 가역이면 A의 역행렬은 유일하다.
증명
행렬 B, C가 모두 A의 역행렬이라면
행렬 B, C가 모두 A의 역행렬이라면
AB=In=BA,
AC=In=CA
이므로AC=In=CA
B=BIn=B(AC)=(BA)C=InC=C ■


![[http]](/123/imgs/http.png)
![[https]](/123/imgs/https.png)