완전 미분 방정식, exact differential equation, exact DE
(정의) 미분방정식
dx+N(x,y)dy=0) ......(1)
......(1)
의 좌변이 어떤 이변수함수 ) 의 전미분
의 전미분 ) 와 같을 때, 즉,
와 같을 때, 즉,
=\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy = M(x,y)dx + N(x,y)dy)
일 때, 식 (1)을 완전미분방정식이라 한다.
이 때, 일반해는=0) 에서
에서 =c) 이다.
이다.
이 때, 일반해는
(판정조건) 미분방정식
dx+N(x,y)dy=0)
이 완전미분방정식이기 위한 필요충분조건은 다음이다.
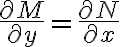
(해법) 완전미분방정식
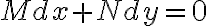
에서
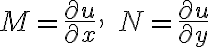
이므로 각각을 적분하여 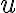 를 찾자. 우선
를 찾자. 우선 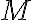 이
이 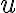 를
를  에 대하여 편미분한 것이므로
에 대하여 편미분한 것이므로 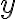 를 상수로 보고
를 상수로 보고 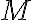 을
을  에 대하여 적분하여
에 대하여 적분하여 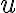 의 일부를 찾는다.
의 일부를 찾는다.
=\int Mdx+k(y)) ......(1)
......(1)
이다. 이 때 ) 는 적분상수의 역할을 한다. 이제 이
는 적분상수의 역할을 한다. 이제 이 ) 를 찾기 위하여 양변을
를 찾기 위하여 양변을 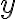 에 대하여 미분한 후
에 대하여 미분한 후 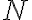 이라 두고 양변을 비교하여
이라 두고 양변을 비교하여 ) 를 찾는다.
를 찾는다.
=N)
이므로
=\int\left( N-\frac{\partial}{\partial y}\int M dx \right) dy)
이다. 이 ) 를 식 (1)에 대입하면, 완전미분방정식의 해공식
를 식 (1)에 대입하면, 완전미분방정식의 해공식
dy=c)
이 얻어진다.
(정보현 공수 p37-38)

