반복하지 않는 시도에서 사건이 발생할 확률분포
크기(=원소의 개수)가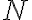 
인 유한한 모집단,population에서,
개의 표본을 "비복원 임의추출"할 때
- 특별한 성질을 가진 것
개 (ex. 성공)
- 특별한 성질을 갖지 않은 나머지
개 (ex. 실패)
확률변수 X : 특별한 성질을 갖고 있는 것들의 개수
X의 확률함수:
=\frac{\binom{k}{x}\binom{N-k}{n-x}}{\binom{N}{n}} "$P(X=x)=\frac{\binom{k}{x}\binom{N-k}{n-x}}{\binom{N}{n}}$")
단 
이면
: 초기하확률변수
의 분포 : 초기하분포
식을 다시 써보면
=\frac{{}_k{\rm C}_x \times {}_{N-k}{\rm C}_{n-x}}{{}_N{\rm C}_n} "$P(X=x)=\frac{{}_k{\rm C}_x \times {}_{N-k}{\rm C}_{n-x}}{{}_N{\rm C}_n}$")
무한모집단에서 표본을 임의추출하거나, 유한모집단에서 복원추출하는 경우, 이항분포 조건을 만족하므로 이항분포를 쓰면 된다. 그러나 유한모집단에서 비복원추출하는 경우, 베르누이_시행,Bernoulli_trial의 조건이 만족되지 않아 이항분포를 사용할 수 없다.
모집단의 크기가 표본의 크기 에 비해 매우 클 때  "$(N\gg n)$")
=\mu=n\frac{k}{N} "$E(X)=\mu=n\frac{k}{N}$")
초기하분포 확률변수 X의 분산:
=\sigma^2=\frac{N-n}{N-1}\cdot n\cdot \frac{k}{N}\cdot\frac{N-k}{N} "$V(X)=\sigma^2=\frac{N-n}{N-1}\cdot n\cdot \frac{k}{N}\cdot\frac{N-k}{N}$")
예)
=\frac{nk}{N}=\frac{5\times3}{40}=\frac38=0.375 "$E(X)=\frac{nk}{N}=\frac{5\times3}{40}=\frac38=0.375$")
=\frac{N-n}{N-1}\cdot n\cdot\frac{k}{N}\cdot\frac{N-k}{N}=\frac{40-5}{40-1}\cdot5\cdot\frac3{40}\cdot\frac{40-3}{40}=0.3113 "$V(X)=\frac{N-n}{N-1}\cdot n\cdot\frac{k}{N}\cdot\frac{N-k}{N}=\frac{40-5}{40-1}\cdot5\cdot\frac3{40}\cdot\frac{40-3}{40}=0.3113$")
(from http://www.kocw.net/home/search/kemView.do?kemId=1162312 4장_확률변수와분포_초기하분포)
근사적으로 이항분포,binomial_distribution 사용 가능
모집단의 크기가 작을 때,이 경우 초기하분포 사용
초기하분포 확률변수 X의 평균:가정: 생산된 40개의 제품 중 실제로 3개의 불량품 존재
5개의 제품을 비복원 임의추출
정확히 1개의 불량품이 발견될 확률?
Sol)5개의 제품을 비복원 임의추출
정확히 1개의 불량품이 발견될 확률?
X: 불량품의 개수
N=40, n=5, k=3인 초기하분포에서 x=1인 경우이므로
=\frac{\binom{3}{1}\binom{37}{4}}{\binom{40}{5}}=0.3011 "$P(X=1)=\frac{\binom{3}{1}\binom{37}{4}}{\binom{40}{5}}=0.3011$")
참고로N=40, n=5, k=3인 초기하분포에서 x=1인 경우이므로
Twin:
![[https]](/123/imgs/https.png)
수학백과: 초기하분포
 "$X\sim \text{HG}(N,m,k)$")
Hypergeometric_distribution
https://everything2.com/title/hypergeometric distribution
수학백과: 초기하분포Hypergeometric_distributionhttps://everything2.com/title/hypergeometric distribution