Difference between r1.2 and the current
@@ -1,3 +1,4 @@
#noindex
함수 $f$ 가 단순 닫힌 경로 $C$ 와 그 안쪽의 모든 점에서 해석적이면 다음이 성립한다. [* https://dreamlab1.tistory.com/m/182]$\int_C f(z)dz=0$
----
@@ -36,9 +37,10 @@
http://blog.naver.com/freshmeat/91343548
Google:코시+구르사+정리
"코시 구르사 정리"
Ndict:"코시 구르사 정리"
Google:"코시 구르사 정리"
----
Up: [[복소해석,complex_analysis]] [[정리,theorem]]
Cauchy-Goursat Theorem
● If  is analytic in a simply connected domain
is analytic in a simply connected domain 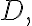
for every simple closed contour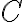 in
in 
dz=0)
or
● If is analytic at all points within and on a simple closed contour
is analytic at all points within and on a simple closed contour 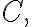 then
then
dz=0)
(Beelee)
for every simple closed contour
● If
Cauchy's Theorem (1825)
Suppose that a function is analytic in a simply connected domain
is analytic in a simply connected domain  and that
and that 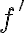 is continuous in
is continuous in 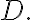 Then for every simple closed contour
Then for every simple closed contour 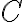 in
in 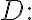
dz=0)
Cauchy-Goursat Theorem (1883)
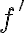 의 연속성을 가정하지 않고도 코시 정리가 성립함을 증명.
의 연속성을 가정하지 않고도 코시 정리가 성립함을 증명.
Suppose a function is analytic in a simply connected domain
is analytic in a simply connected domain 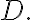 Then for every simple closed contour
Then for every simple closed contour 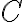 in
in 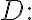
dz=0)
If  is analytic at all points within and on a simple closed contour
is analytic at all points within and on a simple closed contour 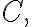 then
then
dz=0.)
(Zill AEM 18.2)
Suppose that a function
Suppose a function
Twins ¶
복소해석에서의 코시 정리 증명 Proof of Cauchy's Theorem
https://freshrimpsushi.github.io/posts/proof-of-cauchys-theorem/
https://freshrimpsushi.github.io/posts/proof-of-cauchys-theorem/

