이하생략
(Thomas Calculus, Riemann Sums)
left hand rule
right hand rule
midpoint rule ... https://www.sfu.ca/math-coursenotes/Math 158 Course Notes/sec_riemann.html
right hand rule
midpoint rule ... https://www.sfu.ca/math-coursenotes/Math 158 Course Notes/sec_riemann.html
mklink 넓이,area
김도형 ¶
점
정의:  가
가 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 정의되어 있을 때, subinterval의 최대가 0으로 가는 극한
에서 정의되어 있을 때, subinterval의 최대가 0으로 가는 극한
 \Delta x_i)
가 존재하면, 그 값을
dx)
로 나타내고,  에서
에서 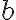 까지
까지  의 정적분,definite_integral이라 한다.
의 정적분,definite_integral이라 한다.
위 극한이 존재할 때, 는
는 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 적분가능이라 한다.
에서 적분가능이라 한다.
i.e.
dx=\lim_{\operatorname{max} \Delta x_i \to 0} \sum_{i=1}^n f(x_i^{\ast}) \Delta x_i)
위 극한이 존재할 때,
i.e.
mklink: 리만_적분,Riemann_integral
Twins:
![[https]](/123/imgs/https.png) 수학백과: 리만 합
수학백과: 리만 합
 Riemann_sum - 적분값을 유한합,finite_sum으로 근사,approximation한 것.
Riemann_sum - 적분값을 유한합,finite_sum으로 근사,approximation한 것.
 리만_합
리만_합
https://mathworld.wolfram.com/RiemannSum.html
https://everything2.com/title/Riemann Sum
![[https]](/123/imgs/https.png) 수학백과: 리만 합
수학백과: 리만 합https://mathworld.wolfram.com/RiemannSum.html
https://everything2.com/title/Riemann Sum
Up:

