미분,differential의 비,ratio, 비율,rate, 분수,fraction 꼴로 나타내는 이것은.... 평균변화율의 극한 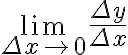 와 같은? 따라서 순간변화율과 같은 뜻의 단어?? CHK
와 같은? 따라서 순간변화율과 같은 뜻의 단어?? CHK
TODO 도함수(미분,derivative)과의 정확한 관계?
미분계수가 0이거나 없는(? CHK) 경우는 임계점,critical_point 참조.
QQQ 미분형식,differential_form과 관계 TBW
Thomas ¶
점 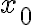 에서 증분
에서 증분 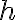 인 함수의 차분몫(difference quotient of
인 함수의 차분몫(difference quotient of  at
at 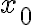 with increment
with increment 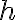 ):
):
-f(x_0)}{h},\;h\ne 0)
함수  의 점
의 점 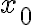 에서 미분계수
에서 미분계수 ) 는 극한값이 존재한다는 조건 하에서
는 극한값이 존재한다는 조건 하에서
=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h})
이다. (13e 번역판 p66-67)
/// 이걸 thomas에서 봤었나? 옳은지 chk
미분계수는 차분몫,difference_quotient의 극한.
비례식 모양을 써서 비유를 하자면 다음 네가지 이것들의 관계는...
미분계수는 차분몫,difference_quotient의 극한.
비례식 모양을 써서 비유를 하자면 다음 네가지 이것들의 관계는...
차분몫 : 미분계수 = 평균변화율 : 순간변화율(콜론의 왼쪽에 극한을 취하면 오른쪽)


![[https]](/123/imgs/https.png)