// ㄷㄱㄱ Week 8-1
joint_probability :![$\text{Pr}[X,Y]$ $\text{Pr}[X,Y]$](/123/cgi-bin/mimetex.cgi?\Large \text{Pr}[X,Y])
joint CDF :![$F_{X,Y}(x,y)=\text{Pr}[X\le x,Y\le y]$ $F_{X,Y}(x,y)=\text{Pr}[X\le x,Y\le y]$](/123/cgi-bin/mimetex.cgi?\Large F_{X,Y}(x,y)=\text{Pr}[X\le x,Y\le y])
joint_probability :
joint CDF :
Joint CDF의 성질들
- When
and
; marginal cdf
사실는 당연한 거라서
이고 위의
이며, 즉 X에 대한 것만이 되며, 이것을 marginal cdf 라고 한다
marginal_cdf는 아마 다음 페이지명으로 - 주변누적분포함수,marginal_cumulative_distribution_function,marginal_CDF
(mklink: 주변확률,marginal_probability
and 주변확률분포,marginal_probability_distribution
and 주변확률밀도함수,marginal_probability_density_function,marginal_PDF
and 누적분포함수,cumulative_distribution_function,CDF
and 결합누적분포함수,joint_cumulative_distribution_function,joint_CDF)
즉 대충… '무한으로 뻗어갈 때' X, Y가 같은 방향이면 1, 반대 방향이면 0, 그 외의 경우는 결정불가능?
For 2-random variable ,\;-\infty<x,y<\infty,)
=P_{X,Y}(X\le x_1, Y\le y_1))
는 joint cdf of )
성질
1. CDF(누적분포함수)이므로 비감소함수.
=F_{X,Y}(-\infty,y_1)=0)
and
=1)
3.
=P(X\le x_1)=F_{X,Y}(x_1,\infty))
=P(Y\le y_1)=F_{X,Y}(\infty,y_1))
related; marginal_CDF
4.
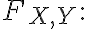 continuous from north and east
continuous from north and east
5.
=F_{X,Y}(x_2,y_2)-F_{X,Y}(x_1,y_2)-F_{X,Y}(x_2,y_1)+F_{X,Y}(x_1,y_1))
이건 2차원 그림을 생각하면 당연.
from 경북대 http://www.kocw.net/home/search/kemView.do?kemId=1279832 4. Joint cdf
1. CDF(누적분포함수)이므로 비감소함수.
For 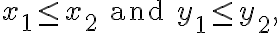
\le F_{X,Y}(x_2,y_2))
2.and
related; marginal_CDF
이건 2차원 그림을 생각하면 당연.


![[http]](/123/imgs/http.png)