주변 분포, marginal distribution
하나의확률변수에 대한 정보만 뽑아내는 것????? CHK
두 변수로 이루어진 결합확률분포를 하나의 변수로 표현하기 위한 것.
두 변수로 이루어진 결합확률분포를 하나의 변수로 표현하기 위한 것.
결합확률분포 ) 가 확률변수
가 확률변수  또는
또는  만의 분포이면
만의 분포이면
확률변수가 이산확률변수,discrete_random_variable일 경우
=\sum_y f(x,y))
=\sum_x f(x,y))
확률변수가 연속확률변수,continuous_random_variable일 경우
=\int_{-\infty}^{\infty} f(x,y)dy)
=\int_{-\infty}^{\infty} f(x,y)dx)
만약 두 확률변수 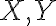 가 독립이면 다음 성질을 가짐.
가 독립이면 다음 성질을 가짐.
=f_X(x)\cdot f_Y(y))
확률변수가 이산확률변수,discrete_random_variable일 경우
X와 Y가 결합확률질량함수,joint_probability_mass_function,joint_PMF ) 인 이산형 결합분포(see 결합확률분포,joint_probability_distribution)를 가질 때,
인 이산형 결합분포(see 결합확률분포,joint_probability_distribution)를 가질 때,
X의 주변확률질량함수
=P(X=x)=\sum_{y}P(X=x,Y=y)=\sum_{y}f(x,y))
Y의 주변확률질량함수
=P(Y=y)=\sum_{x}P(X=x,Y=y)=\sum_{x}f(x,y))
이산형이 아니고 연속형일 땐,
X의 주변확률밀도함수
=\int_{-\infty}^{\infty}f(x,y)dy,\quad -\infty<x<\infty)
Y의 주변확률밀도함수
=\int_{-\infty}^{\infty}f(x,y)dx,\quad -\infty<y<\infty)
seealso
주변 확률 밀도 함수(marginal probability density function) - int
주변 확률 질량 함수(marginal probability mass function) - sum
X의 주변확률질량함수
X의 주변확률밀도함수
주변 확률 밀도 함수(marginal probability density function) - int
주변 확률 질량 함수(marginal probability mass function) - sum


![[https]](/123/imgs/https.png)