기호 a, ac, 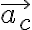
일단은 등속원운동,uniform_circular_motion을 가정
구심가속도는
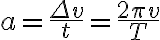
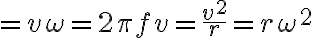
Recall that:
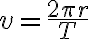
이므로 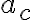 에 대입하면
에 대입하면
^2}{rT^2}=\frac{4\pi^2 r^2}{rT^2}=\frac{4\pi^2 r}{T^2})
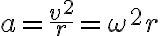
(Pearson Physics Student Edition 2009)
구심가속도
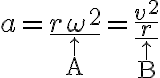
A, B는 손등, 손바닥 같은 관계라서 둘 중 하나를 썼으면 나머지를 쓰지 말아야 한다. (밑의 구심력 식에서도 마찬가지)
(전민용)

