등비급수, 기하급수
아래에 등비급수 .. merge
기하급수 = (무한)등비급수 인가? CHK
실수 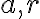 에 대해
에 대해
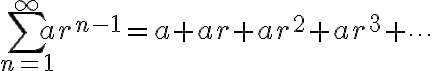
꼴의 급수를 기하급수 또는 (무한)등비급수라고 한다.
수렴 여부는  에 의해 결정된다.
에 의해 결정된다.
(1) 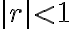 이면 위 급수는
이면 위 급수는 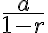 로 수렴한다.
로 수렴한다.
(2)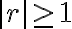 이면 위 급수는 발산한다.
이면 위 급수는 발산한다.
(2)
.... 또는 시작을 0부터 해서 (TBW, CHK)
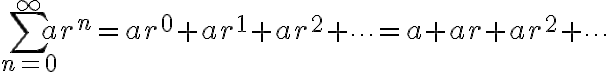
i.e.
정리. 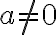 일 때
일 때
 \\ \textrm{diverge} & (|r|\ge 1)\end{cases})
}
관련:
무한등비수열과 무한등비급수의 수렴 조건의 차이
무한등비수열 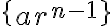 의 수렴 조건:
의 수렴 조건:
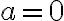 또는
또는 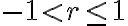
무한등비급수 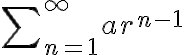 의 수렴 조건:
의 수렴 조건:
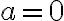 또는
또는 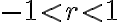
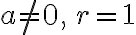 일 경우,
일 경우,
무한등비수열은 첫째항 의 값으로 수렴하지만,
의 값으로 수렴하지만,
무한등비급수는 계속 가 더해져 발산한다.
가 더해져 발산한다.
무한등비수열은 첫째항
무한등비급수는 계속
Related:
수렴,convergence
수열,sequence > 무한수열,infinite_sequence and 등비수열=기하수열,geometric_sequence : 무한등비수열
급수,series > 무한급수,infinite_series and 등비급수=기하급수,geometric_series : 무한등비급수
수렴,convergence
수열,sequence > 무한수열,infinite_sequence and 등비수열=기하수열,geometric_sequence : 무한등비수열
급수,series > 무한급수,infinite_series and 등비급수=기하급수,geometric_series : 무한등비급수
Up: 급수,series

