Difference between r1.28 and the current
@@ -50,11 +50,17 @@
https://blog.naver.com/lyb0684/221332307807https://sasamath.com/blog/articles/finding-lengths-of-axis-ellipse-lagrangian-method/
https://freshrimpsushi.github.io/posts/lagrangian-multiplier-in-optimization-theory/
https://aerospacekim.tistory.com/14
tmp bmks en:
https://tutorial.math.lamar.edu/classes/calciii/lagrangemultipliers.aspx
https://medium.com/@andrew.chamberlain/a-simple-explanation-of-why-lagrange-multipliers-works-253e2cdcbf74
https://machinelearningmastery.com/a-gentle-introduction-to-method-of-lagrange-multipliers/
Understanding Lagrange Multipliers Visually - YouTube
https://www.youtube.com/watch?v=5A39Ht9Wcu0
related:
[[최적화,optimization]]
@@ -68,11 +74,12 @@
이것('''LM''')으로 [[코시-슈바르츠_부등식,Cauchy-Schwartz_inequality]] 증명 가능.표현
라그랑주 승수법 Lagrange multiplier method
Lagrange multiplier method 라그랑주 곱셈자방법
Lagrange multiplier:
라그랑주 승수, 라그랑주 곱셈자
Lagrange multiplier method:
라그랑주 승수법, 라그랑주 곱셈자방법
(기타: 라그랑지 곱수)Ggl:"lagrange undetermined multiplier"
----
[[WpKo:라그랑주_승수법]]
@@ -81,5 +88,5 @@
https://mathworld.wolfram.com/LagrangeMultiplier.htmlUp: [[다변수미적분,multivariable_calculus]] [[최적화,optimization]]
multiplier { WtEn:multiplier }
대략, 어떤 제약,constraint / 제약조건 내에서, 목적함수,objective_function의 최대최소를 찾는 그런 방법?
optimum을 찾는 방법은 아니고, optimum이 되기 위한 조건을 찾는 방법. 즉, 최적해의 필요조건을 찾는 방법. - from https://untitledtblog.tistory.com/96 첫부분, chk
optimum을 찾는 방법은 아니고, optimum이 되기 위한 조건을 찾는 방법. 즉, 최적해의 필요조건을 찾는 방법. - from https://untitledtblog.tistory.com/96 첫부분, chk
Thomas 13e ko p735; tmp - 더 나은 설명으로 교체할 것 ¶
...이 방법은
제약조건=0) 을 만족하는 변수 중에서
을 만족하는 변수 중에서
함수) 의 극대값,(curr see 극값,extremum)은
의 극대값,(curr see 극값,extremum)은
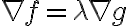
를 만족하는 곡면,surface 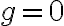 위의 점,point에서 얻어진다는 것이다.
위의 점,point에서 얻어진다는 것이다.
여기서 는 적당한 상수이다. (라그랑주 승수라고 부른다.)
는 적당한 상수이다. (라그랑주 승수라고 부른다.)
제약조건
함수
여기서
tmp; ㄷㄱㄱ Week 14-1 ¶
(거기에 같은 내용 중복, del ok)
다음 constrained NLP를 생각
![$L(\vec{x},\vec{\lambda})=f(\vec{x})+\sum_{j=1}^k \lambda_j \left[ b_j - g_j(\vec{x}) \right]$ $L(\vec{x},\vec{\lambda})=f(\vec{x})+\sum_{j=1}^k \lambda_j \left[ b_j - g_j(\vec{x}) \right]$](/123/cgi-bin/mimetex.cgi?\Large L(\vec{x},\vec{\lambda})=f(\vec{x})+\sum_{j=1}^k \lambda_j \left[ b_j - g_j(\vec{x}) \right])
우변의 오른쪽의 시그마 항은 'penalty term'으로 해석된다.
다음 constrained NLP를 생각
Maximize )
Subject to \le b_j \;\;\;\text{for }\; j=1,2,\ldots,k)
그러면 NLP의 Lagrangian function은 이렇게 정의.Subject to
with 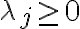 for
for 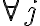
3D의 경우, 오장헌 ¶
그런데 최대/최소 조건이 있으면 관계가 특별해진다.
식들을 명시적으로 표현하면
tmp links ko:
https://untitledtblog.tistory.com/96
https://ratsgo.github.io/convex optimization/2018/01/25/duality/
https://mathphysics.tistory.com/498?category=688910 - 중간부터
https://blog.naver.com/lyb0684/221332307807
https://untitledtblog.tistory.com/96
- geometric 설명 2. 전미분,total_differential 설명
https://ratsgo.github.io/convex optimization/2018/01/25/duality/
https://mathphysics.tistory.com/498?category=688910 - 중간부터
https://blog.naver.com/lyb0684/221332307807
tmp bmks en:
https://tutorial.math.lamar.edu/classes/calciii/lagrangemultipliers.aspx
https://medium.com/@andrew.chamberlain/a-simple-explanation-of-why-lagrange-multipliers-works-253e2cdcbf74
https://machinelearningmastery.com/a-gentle-introduction-to-method-of-lagrange-multipliers/
Understanding Lagrange Multipliers Visually - YouTube
https://www.youtube.com/watch?v=5A39Ht9Wcu0
https://tutorial.math.lamar.edu/classes/calciii/lagrangemultipliers.aspx
https://medium.com/@andrew.chamberlain/a-simple-explanation-of-why-lagrange-multipliers-works-253e2cdcbf74
https://machinelearningmastery.com/a-gentle-introduction-to-method-of-lagrange-multipliers/
Understanding Lagrange Multipliers Visually - YouTube
https://www.youtube.com/watch?v=5A39Ht9Wcu0
maybe related: ...rel?
전미분,total_differential
기울기벡터,gradient_vector
선형계획법,linear_programming
LM을 더 일반화 한 방법: KKT_조건,KKT_condition
전미분,total_differential
기울기벡터,gradient_vector
선형계획법,linear_programming
LM을 더 일반화 한 방법: KKT_조건,KKT_condition
이것(LM)으로 코시-슈바르츠_부등식,Cauchy-Schwartz_inequality 증명 가능.
표현
Lagrange multiplier:
라그랑주 승수, 라그랑주 곱셈자
Lagrange multiplier method:
라그랑주 승수법, 라그랑주 곱셈자방법
(기타: 라그랑지 곱수)
 lagrange undetermined multiplier
lagrange undetermined multiplier
Lagrange multiplier:
라그랑주 승수, 라그랑주 곱셈자
Lagrange multiplier method:
라그랑주 승수법, 라그랑주 곱셈자방법
(기타: 라그랑지 곱수)

