현실을 모델링
See 확률및랜덤프로세스
다음은 시간을 픽스.
and for fixed=X_k "$t=t_k,\;X(t_k,\forall\zeta)=X_k$")
: random variable
and for fixed
then, ,t\in I\rbrace\equiv X(t),\quad t\in I "$\lbrace X(t,\forall\zeta\in S),t\in I\rbrace\equiv X(t),\quad t\in I$")
가
⇔ random process, r.p., 확률과정
여기서 만약 countable set이면,  "$X(t)$")
는 discrete-time r.p. (이산시간확률과정)
continuous set이면, 는 continuous-time r.p. (연속시간확률과정)
from http://www.kocw.net/home/search/kemView.do?kemId=1279832 22. Random process 1:11continuous set이면,
Def.
For continuous-time random process , "$X(t),$")
(i) the mean function  "$m_X(t)$")
of random process : "$X(t):$")
=E(X(t))=\int_{-\infty}^{\infty}xf_{X(t)}(x)dx "$m_X(t)=E(X(t))=\int_{-\infty}^{\infty}xf_{X(t)}(x)dx$")
(ii) the variance function ) "$VAR(X(t))$")
of random process
)=\int_{-\infty}^{\infty}\left{x-m_X(t)\right}^2 f_{X(t)}(x)dx "$VAR(X(t))=\int_{-\infty}^{\infty}\left{x-m_X(t)\right}^2 f_{X(t)}(x)dx$")
}(x)dx-m_X(t)^2 "$=\int_{-\infty}^{\infty}x^2 f_{X(t)}(x)dx-m_X(t)^2$")
(iii) the autocorrelation  "$R_X(t_1,t_2)$")
of random process
=X_1,X(t_2)=X_2 "$X(t_1)=X_1,X(t_2)=X_2$")
일 때
=E\left(X(t_1)X(t_2)\right)=E(X_1X_2)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_{X_1,X_2}(x,y)dxdy "$R_X(t_1,t_2)=E\left(X(t_1)X(t_2)\right)=E(X_1X_2)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_{X_1,X_2}(x,y)dxdy$")
=E\left(X(t)^2\right) "$\to R_X(t,t)=E\left(X(t)^2\right)$")
(iv) the autocovariance  "$C_X(t_1,t_2)$")
of random process
일 때
=E\left(\left(X(t_1)-m_X(t_1)\right)\left(X(t_2)-m_X(t_2)\right)\right) "$C_X(t_1,t_2)=E\left(\left(X(t_1)-m_X(t_1)\right)\left(X(t_2)-m_X(t_2)\right)\right)$")
-m_X(t_1)m_X(t_2) "$=R_X(t_1,t_2)-m_X(t_1)m_X(t_2)$")
X(t_2))-m_X(t_1)m_X(t_2) "$=E(X(t_1)X(t_2))-m_X(t_1)m_X(t_2)$")
=VAR(X(t)) "$\to C_X(t,t)=VAR(X(t))$")
(v) the correlation coefficient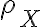 
of random process
=\frac{C_X(t_1,t_2)}{\sqrt{C_X(t_1,t_1)}\times\sqrt{C_X(t_2,t_2)}} "$\rho_X(t_1,t_2)=\frac{C_X(t_1,t_2)}{\sqrt{C_X(t_1,t_1)}\times\sqrt{C_X(t_2,t_2)}}$")
see also 상관계수,correlation_coefficient
여기서  "$f_{X_1,X_2}(x,y)$")
는 joint pdf of X1 and X2
from 23. Specifying a Random Process
Up: 과정,process
----
- [1] 이 그래프는 이름이 여러가지임. sample path(표본경로), sample function(표본함수), realization of random process(확률 과정의 실현)