줄여서 aux eqn
Ex.
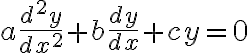
의 보조방정식은

그래서 이차방정식,quadratic_equation의 근의 공식 quadratic_formula 으로 풀어서 그것이 (다른 두 실근인지/중근인지/다른 두 허근인지)에 따라 원래 방정식의 해가 세 형태 중 하나로 정해진다.
설명 1 ¶
상수계수 2계 1차 상미분방정식 (선형 상미분방정식)
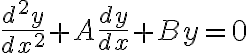
i.e.
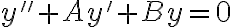
의 보조방정식은
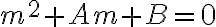
이고, 이 방정식의 근에 따라
1. 두 실근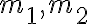

2. 중근 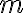
)
3. 허근 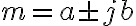
)
)
via https://www.youtube.com/watch?v=wtJG2_jhkew
1. 두 실근
Ex 1 - 응용 ¶
series RLC회로,RLC_circuit system 해석,
spring+mass+damper system 해석,
등등.
{
Example 1
RLC회로,RLC_circuit의 경우 방정식은 다음과 같다.
KVL에 의해
)
i.e.
)
Example 2
spring+mass+damper system { 정확한이름?? pagename TBD. Mass-spring-damper_model ...
Mass-spring-damper_model ...  spring mass damper system } 의 경우 외부 힘(external force)이 없을 때
spring mass damper system } 의 경우 외부 힘(external force)이 없을 때
이 세 힘의 합은 0이므로, 방정식은 다음과 같다.

(이런 상수계수 2nd order ODE에 대해)
spring+mass+damper system 해석,
등등.
{
Example 1
RLC회로,RLC_circuit의 경우 방정식은 다음과 같다.
KVL에 의해
spring+mass+damper system { 정확한이름?? pagename TBD.
이 세 힘의 합은 0이므로, 방정식은 다음과 같다.
이것의 standard_form 은

where
이것의 auxiliary equation은
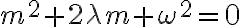
근은
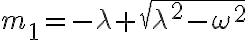
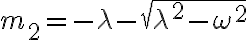
Case I: 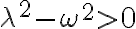 overdamped // overdamping
overdamped // overdamping
=c_1e^{m_1t}+c_2e^{m_2t})
Case II: 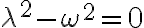 critically damped // critical_damping?
critically damped // critical_damping?
=c_1e^{m_1t}+c_2te^{m_1t})
Case III: 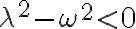 under-damped // underdamping
under-damped // underdamping
=e^{-\lambda t}\left( c_1\cos\sqrt{\omega^2-\lambda^2}t + c_2\sin\sqrt{\omega^2-\lambda^2} t \right))
위 셋의 특성은 각각,
Case I: takes a long time to reach equilibrium
Case II: no overshoot, reach equilibrium in shortest time
Case III: overshoot 존재, oscillates for a while
이것의 auxiliary equation은
Case I: takes a long time to reach equilibrium
Case II: no overshoot, reach equilibrium in shortest time
Case III: overshoot 존재, oscillates for a while
(Beelee)
}
https://everything2.com/title/Auxiliary equation
...
Up: 방정식,equation

