반응속도법칙, 반응 속도 법칙, 반응속도식, 속도식
일정한 온도에서 일어나는 반응
 : 속도상수,rate_constant
: 속도상수,rate_constant
지수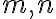 은 반응차수(reaction order)
은 반응차수(reaction order)
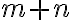 : 전체반응차수(overall reaction order)
: 전체반응차수(overall reaction order)
실험적 결정에는 초기속도방법이 있는데 (method of initial rate)
초기속도를 쓰는 이유는 화학반응이 가역적이므로 역반응에서 오는 복잡함을 피하기 위함.
Q: 반응속도식에 반응물농도만 있고 생성물농도가 없다는게, 초기속도방법을 쓴다는 뜻인가?
aA + bB + … → 생성물(들)
의 속도법칙은속도 = rate = ![$k[{\rm A}]^m[{\rm B}]^n...$ $k[{\rm A}]^m[{\rm B}]^n...$](/123/cgi-bin/mimetex.cgi?\Large k[{\rm A}]^m[{\rm B}]^n...)
여기서,지수
A, B의 농도에 얼마나 민감한지를 보여줌 (e.g. m<n이면 B의 농도에 더 민감)
실험에 의해 결정되는 것임. (determined by experiment)
a, b와 무관하며 반응의 화학량론 계수 a, b에서 유추할 수 없음.
ex.
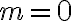 : 속도는
: 속도는 ![$[{\rm A}]$ $[{\rm A}]$](/123/cgi-bin/mimetex.cgi?\Large [{\rm A}]) 와 무관
와 무관
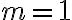 : 속도는
: 속도는 ![$[{\rm A}]$ $[{\rm A}]$](/123/cgi-bin/mimetex.cgi?\Large [{\rm A}]) 에 비례
에 비례
etc.
실험에 의해 결정되는 것임. (determined by experiment)
a, b와 무관하며 반응의 화학량론 계수 a, b에서 유추할 수 없음.
ex.
etc.
초기속도를 쓰는 이유는 화학반응이 가역적이므로 역반응에서 오는 복잡함을 피하기 위함.
Q: 반응속도식에 반응물농도만 있고 생성물농도가 없다는게, 초기속도방법을 쓴다는 뜻인가?
2. 속도법칙의 종류 ¶
미분속도법칙 differential rate law
반응속도 = f(농도), rate=f(conc)
적분속도법칙농도 = f(시간), conc=f(time)
(이하 Masterton)

![[https]](/123/imgs/https.png)