화학 반응 속도론, 반응 속도론, reaction kinetics, chemical kinetics
화학반응,chemical_reaction 속도(rate, 농도변화÷시간) 에 대한 이론
화학반응,chemical_reaction 속도(rate, 농도변화÷시간) 에 대한 이론
wpko에 의하면
화학속도론 chemical kinetics
반응속도론 reaction kinetics
화학반응속도론 chemical reaction kinetics
물리학회 용어집에 의하면반응속도론 reaction kinetics
화학반응속도론 chemical reaction kinetics
반응 운동학 reaction kinetics
반응 속도론 chemical kinetics
Sub:반응 속도론 chemical kinetics
반응속도,reaction_rate
속도상수,rate_constant
속도법칙,rate_law
아레니우스_식,Arrhenius_equation
활성화에너지,activation_energy
효소반응속도론,enzyme_kinetics w
속도상수,rate_constant
속도법칙,rate_law
아레니우스_식,Arrhenius_equation
활성화에너지,activation_energy
효소반응속도론,enzyme_kinetics w
Contents
1.2. 단어 ¶
전이 상태 transition state
활성화물 activated complex
촉매 작용 catalysis
촉매 catalyst
catalytic 촉매의, 촉매작용의
활성화물 activated complex
촉매 작용 catalysis
촉매 catalyst
catalytic 촉매의, 촉매작용의
반감기는 ![$[{\rm A}]=\frac{[{\rm A_0}]}{2}$ $[{\rm A}]=\frac{[{\rm A_0}]}{2}$](/123/cgi-bin/mimetex.cgi?\Large [{\rm A}]=\frac{[{\rm A_0}]}{2}) 가 되는 t이며,
가 되는 t이며,
즉 A의 농도가 초기 농도 A0의 절반이 되는 시간이며,
기호는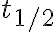 인게 맞는지 CHK
인게 맞는지 CHK
즉 A의 농도가 초기 농도 A0의 절반이 되는 시간이며,
기호는
2. 시작 ¶
일단
반응속도론은 영어로 kinetics(운동학)이며, 여기서 속도는 rate이다. (speed라고도 하지만 velocity는 절대 아님)
반응속도 reaction rate 반응속도,reaction_rate
반응속도상수 reaction rate constant = 속도상수 rate constant (= 반응상수 ? reaction constant ??? ) - k, k(T) 속도상수,rate_constant
속도법칙 rate law 속도법칙,rate_law
반응속도식 rate equation
반응차수 reaction order - 보통 알파벳 m, n 등으로 표기
아레니우스 식 Arrhenius equation 아레니우스_식,Arrhenius_equation
- [A]는 A의 몰농도,molarity.
- Δ[A]는 A의 몰농도의 변화.
반응속도론은 영어로 kinetics(운동학)이며, 여기서 속도는 rate이다. (speed라고도 하지만 velocity는 절대 아님)
반응속도 reaction rate 반응속도,reaction_rate
반응속도상수 reaction rate constant = 속도상수 rate constant (= 반응상수 ? reaction constant ??? ) - k, k(T) 속도상수,rate_constant
속도법칙 rate law 속도법칙,rate_law
반응속도식 rate equation
반응차수 reaction order - 보통 알파벳 m, n 등으로 표기
individual order
전체반응차수 overall reaction order (전반응차수) - n+m+...
반응 차수에 따라,전체반응차수 overall reaction order (전반응차수) - n+m+...
영차반응 zero-order reaction - 반응속도가 반응물농도와 무관
일차반응 first-order reaction - 반응속도가 한 가지 반응물농도에만 의존
활성화에너지 activation energy - Ea 활성화에너지,activation_energy일차반응 first-order reaction - 반응속도가 한 가지 반응물농도에만 의존
-Δ[A]/Δt=k[A]
이차반응 second-order reaction - 반응속도가 한 반응물농도의 제곱에 비례하거나, 서로 다른 두 반응물 농도의 곱에 비례-Δ[A]/Δt=k[A]2
n차반응아레니우스 식 Arrhenius equation 아레니우스_식,Arrhenius_equation
4.1. 미분속도식 differential rate law ¶
AKA 미분형 속도 법칙
또는 단순히 속도식 rate law
또는 단순히 속도식 rate law
반응속도가 농도에 어떻게 의존하는가?
속도의 농도에 대한 의존성
속도의 농도에 대한 의존성
반응속도 = f(농도)
rate = f(concentration)
)
rate = f(concentration)
속도 = ![$-\frac{\Delta\textrm{[NO_2]}}{\Delta t}=k[{\rm NO}_2]^n$ $-\frac{\Delta\textrm{[NO_2]}}{\Delta t}=k[{\rm NO}_2]^n$](/123/cgi-bin/mimetex.cgi?\Large -\frac{\Delta\textrm{[NO_2]}}{\Delta t}=k[{\rm NO}_2]^n)
4.2. 적분속도식 integrated rate law ¶
AKA 적분형 속도 법칙
농도가 시간에 어떻게 의존하는가?
농도의 시간에 대한 의존성
농도의 시간에 대한 의존성
농도 = f(시간)
concentration = f(time)
)
concentration = f(time)
5.1. 표 ¶
| 반응차수 | 미분형속도법칙 | 적분형속도법칙 |
| 영차반응 | ||
| 일차반응 | ||
| 이차반응 |
| 0차반응 | 1차반응 | 2차반응 | |
| (미분)속도법칙 | |||
| 적분속도법칙 | |||
| 속도상수 k의 단위 | M/s | 1/s | 1/(M·s) |
| Linear plot to determine k | |||
| 반감기,half-life |
6. 속도법칙 ¶
패턴: ... CHK
그리고 반감기도 구한다.
각 n차 반응에 대해,
(변화율) = k(초기농도)n 식을 쓰고
변수분리하고
양변을 적분한다.
끝에서는 x축을 시간 t로 하는 그래프를 그린다.(변화율) = k(초기농도)n 식을 쓰고
변수분리하고
양변을 적분한다.
그리고 반감기도 구한다.
이 섹션에 대해선 별도의 페이지도 있으므로 같이 참조. (속도법칙,rate_law)
6.1. 일차반응 first order reaction ¶
반응속도,reaction_rate가 한 반응물 농도의 1제곱에만 의존하는 반응.
일차반응에서 시간에 대한![$\ln[{\rm A}]_t$ $\ln[{\rm A}]_t$](/123/cgi-bin/mimetex.cgi?\Large \ln[{\rm A}]_t) 의 그래프는
의 그래프는
기울기가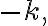 y절편이
y절편이 ![$\ln[{\rm A}]_0$ $\ln[{\rm A}]_0$](/123/cgi-bin/mimetex.cgi?\Large \ln[{\rm A}]_0) 인 직선이다.
인 직선이다.
A → 생성물
형태의 반응에서 일차 반응 속도 법칙은일차반응에서 시간에 대한
기울기가
6.2. 이차반응 second order reaction ¶
전체반응차수가 2차인 반응. A→생성물 또는 A+B→생성물 형태.
반응물이 한가지인 경우 즉
![$1/[{\rm A}]_t$ $1/[{\rm A}]_t$](/123/cgi-bin/mimetex.cgi?\Large 1/[{\rm A}]_t) 의 그래프는
의 그래프는
기울기가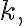 y절편이
y절편이 ![$1/[{\rm A}]_0$ $1/[{\rm A}]_0$](/123/cgi-bin/mimetex.cgi?\Large 1/[{\rm A}]_0) 인 직선.
인 직선.
반응물이 한가지인 경우 즉
A→생성물 (만 살펴보는 듯 한데..)
에서 A에 대해 이차반응일 때, 속도법칙,rate_law은속도 = ![$-\frac{\Delta[{\rm A}]}{\Delta t}=k[{\rm A}]^2$ $-\frac{\Delta[{\rm A}]}{\Delta t}=k[{\rm A}]^2$](/123/cgi-bin/mimetex.cgi?\Large -\frac{\Delta[{\rm A}]}{\Delta t}=k[{\rm A}]^2)
Rate =![$\frac{d[{\rm A}]}{dt}=-k[{\rm A}]^2$ $\frac{d[{\rm A}]}{dt}=-k[{\rm A}]^2$](/123/cgi-bin/mimetex.cgi?\Large \frac{d[{\rm A}]}{dt}=-k[{\rm A}]^2)
![$-\int\nolimits_{[{\rm A}]_0}^{[{\rm A}]}\frac{d[{\rm A}]}{[{\rm A}]^2}=k\int\nolimits_0^t dt$ $-\int\nolimits_{[{\rm A}]_0}^{[{\rm A}]}\frac{d[{\rm A}]}{[{\rm A}]^2}=k\int\nolimits_0^t dt$](/123/cgi-bin/mimetex.cgi?\Large -\int\nolimits_{[{\rm A}]_0}^{[{\rm A}]}\frac{d[{\rm A}]}{[{\rm A}]^2}=k\int\nolimits_0^t dt)
![$\left.\frac1{[{\rm A}]}\right|_{[{\rm A}]_0}^{[{\rm A}]}=\frac1{[{\rm A}]}-\frac1{[{\rm A}]_0}=kt$ $\left.\frac1{[{\rm A}]}\right|_{[{\rm A}]_0}^{[{\rm A}]}=\frac1{[{\rm A}]}-\frac1{[{\rm A}]_0}=kt$](/123/cgi-bin/mimetex.cgi?\Large \left.\frac1{[{\rm A}]}\right|_{[{\rm A}]_0}^{[{\rm A}]}=\frac1{[{\rm A}]}-\frac1{[{\rm A}]_0}=kt)
![$\frac1{[{\rm A}]_t}=kt+\frac1{[{\rm A}]_0}$ $\frac1{[{\rm A}]_t}=kt+\frac1{[{\rm A}]_0}$](/123/cgi-bin/mimetex.cgi?\Large \frac1{[{\rm A}]_t}=kt+\frac1{[{\rm A}]_0})
![$\begin{array}(\frac1{[{\rm A}]_t})&=&(k)t&+&(\frac1{[{\rm A}]_0})\\ \updownarrow&&\updownarrow&&\updownarrow\\y&=&mx&+&b\end{array}$ $\begin{array}(\frac1{[{\rm A}]_t})&=&(k)t&+&(\frac1{[{\rm A}]_0})\\ \updownarrow&&\updownarrow&&\updownarrow\\y&=&mx&+&b\end{array}$](/123/cgi-bin/mimetex.cgi?\Large \begin{array}(\frac1{[{\rm A}]_t})&=&(k)t&+&(\frac1{[{\rm A}]_0})\\ \updownarrow&&\updownarrow&&\updownarrow\\y&=&mx&+&b\end{array})
이차반응에서 시간에 대한 Rate =
기울기가
6.3. 영차 반응 zero order reaction ¶
전체 반응 차수가 0인 반응. A의 반응속도가 [A]와 무관.
![$[{\rm A}]_t=-kt+[{\rm A}]_0$ $[{\rm A}]_t=-kt+[{\rm A}]_0$](/123/cgi-bin/mimetex.cgi?\Large [{\rm A}]_t=-kt+[{\rm A}]_0)
영차반응에서 시간에 대한 ![$[{\rm A}]_t$ $[{\rm A}]_t$](/123/cgi-bin/mimetex.cgi?\Large [{\rm A}]_t) 그래프는
그래프는
기울기가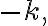 y절편이
y절편이 ![$[{\rm A}]_0$ $[{\rm A}]_0$](/123/cgi-bin/mimetex.cgi?\Large [{\rm A}]_0) 인 직선.
인 직선.
속도 = ![$\frac{-\Delta[{\rm A}]}{\Delta t}=k[{\rm A}]^0=k$ $\frac{-\Delta[{\rm A}]}{\Delta t}=k[{\rm A}]^0=k$](/123/cgi-bin/mimetex.cgi?\Large \frac{-\Delta[{\rm A}]}{\Delta t}=k[{\rm A}]^0=k)
적분하면기울기가
(이상 1~3차반응: Brown 13e)
6.4. 1차반응 적분속도법칙 ¶
적분속도법칙(integrated rate law)
어떤 시간 t에 남아 있는 반응물 농도를 계산할 수 있게 하는 농도-시간 식.
1차반응(first-order reaction) : 속도가 단일 반응물 농도의 1제곱에 의존하는 반응
어떤 시간 t에 남아 있는 반응물 농도를 계산할 수 있게 하는 농도-시간 식.
1차반응(first-order reaction) : 속도가 단일 반응물 농도의 1제곱에 의존하는 반응
A → 생성물 반응에서
A의 소모 속도![$=-\frac{\Delta [{\rm A}]}{\Delta t}=k[{\rm A}]$ $=-\frac{\Delta [{\rm A}]}{\Delta t}=k[{\rm A}]$](/123/cgi-bin/mimetex.cgi?\Large =-\frac{\Delta [{\rm A}]}{\Delta t}=k[{\rm A}])
![$\frac{\Delta [{\rm A}]}{[{\rm A}]}=-k \Delta t$ $\frac{\Delta [{\rm A}]}{[{\rm A}]}=-k \Delta t$](/123/cgi-bin/mimetex.cgi?\Large \frac{\Delta [{\rm A}]}{[{\rm A}]}=-k \Delta t)
![$\frac{\partial [{\rm A}]}{[{\rm A}]}=-k \partial t$ $\frac{\partial [{\rm A}]}{[{\rm A}]}=-k \partial t$](/123/cgi-bin/mimetex.cgi?\Large \frac{\partial [{\rm A}]}{[{\rm A}]}=-k \partial t)
![$\int_{[{\rm A}]_0}^{[{\rm A}]_t}\frac{\partial [{\rm A}]}{[{\rm A}]}=-k\int_0^t\partial t$ $\int_{[{\rm A}]_0}^{[{\rm A}]_t}\frac{\partial [{\rm A}]}{[{\rm A}]}=-k\int_0^t\partial t$](/123/cgi-bin/mimetex.cgi?\Large \int_{[{\rm A}]_0}^{[{\rm A}]_t}\frac{\partial [{\rm A}]}{[{\rm A}]}=-k\int_0^t\partial t)
![$\ln[{\rm A}]_t=-kt+\ln[{\rm A}]_0$ $\ln[{\rm A}]_t=-kt+\ln[{\rm A}]_0$](/123/cgi-bin/mimetex.cgi?\Large \ln[{\rm A}]_t=-kt+\ln[{\rm A}]_0)
![$\ln\frac{[{\rm A}]_t}{[{\rm A}]_0}=-kt$ $\ln\frac{[{\rm A}]_t}{[{\rm A}]_0}=-kt$](/123/cgi-bin/mimetex.cgi?\Large \ln\frac{[{\rm A}]_t}{[{\rm A}]_0}=-kt) (1차반응의 적분속도법칙)
(1차반응의 적분속도법칙)
즉![$\ln[{\rm A}]\leftrightarrow t$ $\ln[{\rm A}]\leftrightarrow t$](/123/cgi-bin/mimetex.cgi?\Large \ln[{\rm A}]\leftrightarrow t) 의 그래프를 그리면 y절편이
의 그래프를 그리면 y절편이 ![$\ln[{\rm A}]_0$ $\ln[{\rm A}]_0$](/123/cgi-bin/mimetex.cgi?\Large \ln[{\rm A}]_0) 이고 기울기가
이고 기울기가 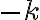 인 감소하는 직선 형태.
인 감소하는 직선 형태.
(항공대)A의 소모 속도
즉
6.5. 1차반응 반감기 ¶
반감기,half-life
![$\ln\frac{[{\rm A}]_t}{[{\rm A}]_0}=-kt$ $\ln\frac{[{\rm A}]_t}{[{\rm A}]_0}=-kt$](/123/cgi-bin/mimetex.cgi?\Large \ln\frac{[{\rm A}]_t}{[{\rm A}]_0}=-kt)
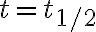 일 때,
일 때, ![$[{\rm A}]_t=\frac12 [{\rm A}]_0$ $[{\rm A}]_t=\frac12 [{\rm A}]_0$](/123/cgi-bin/mimetex.cgi?\Large [{\rm A}]_t=\frac12 [{\rm A}]_0)
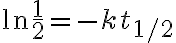

일차반응의 반감기는 반응물 농도와 무관하고 속도상수에만 의존하므로 일정하다.
: 반응물의 농도가 절반으로 떨어지는 데 걸리는(필요한) 시간
기호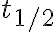
일차반응속도법칙기호
1차 반응의 반감기 유도
농도(C)가 처음 농도(C0)의 1/2가 될때까지 걸리는 시간, 즉

일 때까지 걸리는 시간이 반감기.
 = \ln\left(\frac{C_0/2}{C_0}\right) = -\ln2=-kt)
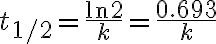
농도(C)가 처음 농도(C0)의 1/2가 될때까지 걸리는 시간, 즉
6.6. 2차반응 적분속도법칙 ¶
적분속도법칙: 2차반응(second-order reaction)
A → 생성물 반응에서
A의 소모 속도![$=-\frac{\Delta [{\rm A}]}{\Delta t}=k[{\rm A}]^2$ $=-\frac{\Delta [{\rm A}]}{\Delta t}=k[{\rm A}]^2$](/123/cgi-bin/mimetex.cgi?\Large =-\frac{\Delta [{\rm A}]}{\Delta t}=k[{\rm A}]^2)
![$\frac{\Delta [{\rm A}]}{[{\rm A}]^2}=-k \Delta t$ $\frac{\Delta [{\rm A}]}{[{\rm A}]^2}=-k \Delta t$](/123/cgi-bin/mimetex.cgi?\Large \frac{\Delta [{\rm A}]}{[{\rm A}]^2}=-k \Delta t)
![$\frac{\partial [{\rm A}]}{[{\rm A}]^2}=-k \partial t$ $\frac{\partial [{\rm A}]}{[{\rm A}]^2}=-k \partial t$](/123/cgi-bin/mimetex.cgi?\Large \frac{\partial [{\rm A}]}{[{\rm A}]^2}=-k \partial t)
![$\int_{[{\rm A}]_0}^{[{\rm A}]_t}\frac{\partial [{\rm A}]}{[{\rm A}]^2}=-k\int_0^t\partial t$ $\int_{[{\rm A}]_0}^{[{\rm A}]_t}\frac{\partial [{\rm A}]}{[{\rm A}]^2}=-k\int_0^t\partial t$](/123/cgi-bin/mimetex.cgi?\Large \int_{[{\rm A}]_0}^{[{\rm A}]_t}\frac{\partial [{\rm A}]}{[{\rm A}]^2}=-k\int_0^t\partial t)
![$\frac{1}{[{\rm A}]_t}-\frac{1}{[{\rm A}]_0}=kt$ $\frac{1}{[{\rm A}]_t}-\frac{1}{[{\rm A}]_0}=kt$](/123/cgi-bin/mimetex.cgi?\Large \frac{1}{[{\rm A}]_t}-\frac{1}{[{\rm A}]_0}=kt)
![$\frac{1}{[{\rm A}]_t}=kt+\frac{1}{[{\rm A}]_0}$ $\frac{1}{[{\rm A}]_t}=kt+\frac{1}{[{\rm A}]_0}$](/123/cgi-bin/mimetex.cgi?\Large \frac{1}{[{\rm A}]_t}=kt+\frac{1}{[{\rm A}]_0}) (y=mx+b 꼴) (2차반응의 적분속도법칙)
(y=mx+b 꼴) (2차반응의 적분속도법칙)
A의 소모 속도
직선의 기울기는 속도상수 k. y절편은
8. 입체인자 p ¶
입체 인자(steric factor) 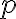
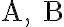 분자 사이의 이분자 충돌반응에서
분자 사이의 이분자 충돌반응에서
반응물에서 생성물로 변화되기에 적절한 배향(orientation)을 가지는 충돌의 분율
충돌속도 = ![$Z[\textrm{A}][\textrm{B}]$ $Z[\textrm{A}][\textrm{B}]$](/123/cgi-bin/mimetex.cgi?\Large Z[\textrm{A}][\textrm{B}])
반응속도 = p × f × 충돌속도
![$=pfZ[\textrm{A}][\textrm{B}]=k[\textrm{A}][\textrm{B}]$ $=pfZ[\textrm{A}][\textrm{B}]=k[\textrm{A}][\textrm{B}]$](/123/cgi-bin/mimetex.cgi?\Large =pfZ[\textrm{A}][\textrm{B}]=k[\textrm{A}][\textrm{B}])
속도상수 = )
반응속도 = p × f × 충돌속도
9. 반응 메커니즘 ¶
반응 메커니즘 (reaction mechanism)
A reaction mechanism is a description of a path, or a sequence of steps, by which a reaction occurs at the molecular level. (Masterton)
반응물에서 생성물까지의 반응 단계 순서 (경로)
한 단계는 단일단계반응(elementary reaction) or 단일단계(elementary step)
???? tmp; masterton.
반응물에서 생성물까지의 반응 단계 순서 (경로)
한 단계는 단일단계반응(elementary reaction) or 단일단계(elementary step)
- 단일단계반응(elementary reaction) - 각 개별 분자의 사건을 기술
- 전체반응(overall reaction) - 반응의 화학량론을 기술
| unimolecular | A→B+C |
| bimolecular | A+B→C+D |
| termolecular | A+B+C→D+E |
가장 느린 단계가 속도를 좌우. (the slow step is rate-determining)
반응중간체(reaction intermediate) : 전체 반응의 알짜 반응식에는 나타나지 않음

