복원력은 용수철 상수(spring constant) k와 변위 x의 곱에 비례.
-부호 : 작용하는 힘과 변형된 방향이 반대임을 의미
관련내용. (tmp, cleanup and/or del ok)
{
x : displacement from equilibrium
{
F = −kx 에서k : spring constant
x : displacement from equilibrium
대충 이것들의 관계를 설명하는 법칙인데...
스프링/용수철/spring 상수 (k)
질량,mass(이 있는 물체) (m)
평형,equilibrium위치에서부터의 변위,displacement (x)
힘,force (F)
(명확히 rewrite)
스프링/용수철/spring 상수 (k)
질량,mass(이 있는 물체) (m)
평형,equilibrium위치에서부터의 변위,displacement (x)
힘,force (F)
(명확히 rewrite)
그래서 이걸 설명하는 방정식은 이계선형상미분방정식 second-order_linear_ODE (curr 상미분방정식,ordinary_differential_equation,ODE)
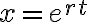
특성방정식,characteristic_equation:
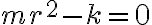
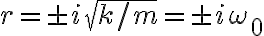
여기서 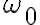 : 기본주파수,fundamental_frequency or 기본진동수,fundamental_frequency
: 기본주파수,fundamental_frequency or 기본진동수,fundamental_frequency
일반해,general_solution:
 + B\sin(\omega_0 t))
그리고 이것을 다음과 같이 하나의 cosine으로 나타낼 수 있음 (4m)
)
(from Bazett, https://www.youtube.com/watch?v=Z52emur7Rko)
}
mx′′+kx=0해,solution의 형태를 추측(guess):
일반해,general_solution:
}
탄성퍼텐셜에너지 ¶
(고딩 물1 교과서에서)
탄성력에 의한 위치에너지
AKA 탄성에너지
탄성력에 의한 위치에너지
AKA 탄성에너지
용수철을 늘이는 데 필요한 힘,force은 늘어난 길이  에 비례.
에 비례.
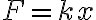
길이가  만큼 늘어난 용수철이 원래 길이로 되돌아가려는 탄성력은
만큼 늘어난 용수철이 원래 길이로 되돌아가려는 탄성력은
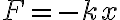
용수철 길이를 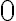 에서
에서  까지 늘이는 동안, 용수철에 작용하는 힘은
까지 늘이는 동안, 용수철에 작용하는 힘은 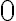 에서
에서 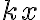 까지 증가.
까지 증가.
따라서 그 동안 용수철에 한 일,work은, 이 동안에 작용한 힘의 평균,mean,average 에 늘어난 길이
에 늘어난 길이  를 곱한 것과 같으므로
를 곱한 것과 같으므로
\cdot x = \frac12 kx^2)
일반적으로  만큼 변형된 용수철이 가지는 탄성력에 의한 위치에너지는
만큼 변형된 용수철이 가지는 탄성력에 의한 위치에너지는
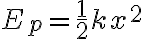
(적분을 안하고 힘이 항상 일정함을 가정해서 이렇게 처리)
따라서 그 동안 용수철에 한 일,work은, 이 동안에 작용한 힘의 평균,mean,average
훅 법칙에 가속도법칙 적용한 미방의 해 ¶
links ko ¶
Related:
외부의 힘에 의해 변형된 물체가 이 힘이 제거되었을 때 원래의 상태로 되돌아가려고 하는 성질.
반대로 외부 힘이 제거되었는데도 원래 모양으로 되돌아가지 않고 변형된 상태에 머무르는 성질을 소성(plasticity)이라 함.
}
Up:
외부의 힘에 의해 변형된 물체가 이 힘이 제거되었을 때 원래의 상태로 되돌아가려고 하는 성질.
반대로 외부 힘이 제거되었는데도 원래 모양으로 되돌아가지 않고 변형된 상태에 머무르는 성질을 소성(plasticity)이라 함.
}
Up:

