Subtopics ¶
운동,motion
모멘트,moment - 운동량과 스펠링 비슷...관계는?
충격량,impulse I, J
충격량과_운동량
운동량보존법칙
충돌,collision
직선운동,linear_motion
병진운동,translational_motion
진동운동,oscillatory_motion
회전운동,rotational_motion
원운동,circular_motion
포물선운동,projectile_motion
etc.
운동량,momentum병진운동,translational_motion
진동운동,oscillatory_motion
회전운동,rotational_motion
원운동,circular_motion
포물선운동,projectile_motion
etc.
모멘트,moment - 운동량과 스펠링 비슷...관계는?
충격량,impulse I, J
충격량과_운동량
운동량보존법칙
충돌,collision
에너지,energy E, U, Ek
변위,displacement, 거리,distance, 길이,length (폭 너비 width, 높이 height, 고도 altitude, 두께 thickness, 깊이 depth, …)
속도,velocity - 시간에 따른 변위,displacement
- 시간에 따른 변위,displacement
속력,speed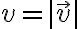 - 시간에 따른 거리,distance변화
- 시간에 따른 거리,distance변화
가속도,acceleration
가속력?
속도,velocity
속력,speed
가속도,acceleration
가속력?
속도 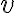 의 절대값
의 절대값 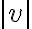 를 속력이라 한다.
를 속력이라 한다.
가속도 의 절대값
의 절대값  를 가속력이라 한다. (정석 수2 p. 139)
를 가속력이라 한다. (정석 수2 p. 139)
가속도
1법칙 관성,inertia의 법칙: 물체는 알짜힘,force=0이면 운동 상태를 유지하려는 특성이 있음
2법칙 가속도 법칙: F=dp/dt=ma, 물체의 가속도,acceleration는 알짜힘,force에 비례하며 질량,mass에 반비례함
3법칙 작용-반작용(action-reaction) 법칙
2법칙 가속도 법칙: F=dp/dt=ma, 물체의 가속도,acceleration는 알짜힘,force에 비례하며 질량,mass에 반비례함
3법칙 작용-반작용(action-reaction) 법칙
1법칙
관성의 법칙

외부 힘이 가해지지 않는 모든 물체는
관성의 법칙
외부 힘이 가해지지 않는 모든 물체는
- 정지해 있거나
- 등속운동 상태를
2법칙

i.e.
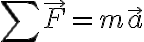
3법칙
1법칙 : 힘이 0인 경우임 (이 때는 속도의 변화가 없음)
2법칙 : 힘이 0이 아닌 경우임 (이 때는 힘이 질량 곱하기 가속도)
3법칙 : (반대 방향의 두 힘? 아님 한 힘이 뭔가에 작용하면 그와 magnitude는 같고 방향,direction은 정반대인 다른 한 힘이 필연적으로 생긴다는? chk) - 암튼 작용(action)과 반작용(reaction).
Forces in nature always exist in pairs.
A single isolated force can't exist.
ex. 수직항력,normal_force: 책상에 놓인 물체의 무게와 그 반작용.
뉴턴의 세 법칙과 힘,force의 관계A single isolated force can't exist.
ex. 수직항력,normal_force: 책상에 놓인 물체의 무게와 그 반작용.
1법칙 : 힘이 0인 경우임 (이 때는 속도의 변화가 없음)
2법칙 : 힘이 0이 아닌 경우임 (이 때는 힘이 질량 곱하기 가속도)
3법칙 : (반대 방향의 두 힘? 아님 한 힘이 뭔가에 작용하면 그와 magnitude는 같고 방향,direction은 정반대인 다른 한 힘이 필연적으로 생긴다는? chk) - 암튼 작용(action)과 반작용(reaction).
Misc
F=ma는 상대성이론,relativity_theory, 양자역학,quantum_mechanics을 고려하면 옳은 식이 아님
}
케플러_법칙,Kepler_s_laws
{
Kepler's laws of planetary motion, Kepler's three laws
1. The Law of Orbits, The Law of Ellipses 타원 궤도 법칙
2. The Law of Areas, The Law of Equal Areas: 면적 속도 일정 법칙
}
F=ma는 상대성이론,relativity_theory, 양자역학,quantum_mechanics을 고려하면 옳은 식이 아님
}
케플러_법칙,Kepler_s_laws
{
Kepler's laws of planetary motion, Kepler's three laws
1. The Law of Orbits, The Law of Ellipses 타원 궤도 법칙
2. The Law of Areas, The Law of Equal Areas: 면적 속도 일정 법칙
공전 속도는 일정하지 않으며 근일점에서 가장 빠르고 원일점에서 가장 느리다
3. The Law of Periods, The Law of Harmonies: 조화 법칙: 공전 주기(T)의 제곱은 타원 궤도 긴반지름(R)의 세제곱에 비례:T2 ∝ R3
행성일 경우근일점,perihelion
원일점,aphelion
특히 지구일 경우원일점,aphelion
근지점,perigee
원지점,apogee
See also 타원,ellipse원지점,apogee
}
Subfields ¶
역학의 주제는,
- 힘을 받는 물체의 평형,equilibrium을 다루는 정역학,statics과
- 물체의 운동,motion을 다루는 동역학,dynamics으로 나뉜다.
운동,motion의 원인에 따라:
{
https://everything2.com/title/Dynamics
https://everything2.com/title/Kinetics
https://everything2.com/title/Kinematics
}
- kinematics: 운동의 원인을 생각하지 않음, 어떻게 기술할 수 있을지 생각함 - 벡터 등
- dynamics: 운동의 원인을 생각 - (그것은 바로 힘) - Newton의 법칙 등
{
https://everything2.com/title/Dynamics
https://everything2.com/title/Kinetics
https://everything2.com/title/Kinematics
}
뉴턴역학 Newtonian mechanics
라그랑주 역학 Lagrangian mechanics - 최소작용원리 least action principle, principle of least action
라그랑주 역학 Lagrangian mechanics - 최소작용원리 least action principle, principle of least action
라그랑주_역학,Lagrangian_mechanics - 최소작용원리,least_action_principle, rel. 변분법,variational_calculus ... 작용,action 원리,principle
해밀턴 역학 Hamiltonian mechanics(Very Easy) 고딩 물I 등가속도직선운동 세 공식 ¶
고등학교 물리I 교과서의 등가속도직선운동 세 공식 유도 과정
가속도는
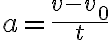
이므로 t초 후의 속도 v는
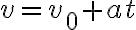
평균속도 = ((처음 속도) + (나중 속도)) / 2

시간 t동안 물체가 s만큼 이동하면, 평균속도는
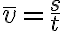
이므로, 이동거리 s는
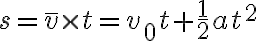
t를 소거하면
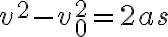
이것도 물리I 교과서의 세 공식 of 등가속도 직선 운동
(1)
(i.e. 처음(t=0)에 속도 v0로 운동하다가, 일정한 가속 후, 시각 t에서 속도 v로 되었다면)
가속도 a는
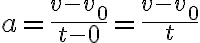
따라서 t초 후의 속도 v는
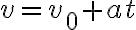
(2)
다음, 속도가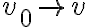 로 변할 때까지 이동한 거리 s는
로 변할 때까지 이동한 거리 s는
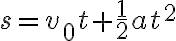
(설명에 그림이 필요하여 생략. 그냥 v-t그래프에서 속도가 v0에서 v로 올라가는 사다리꼴 넓이 구하는 방법.)
| 시각 | 속도 | |
| 처음 | 0 | v0 |
| 현재 | t | v |
가속도 a는
다음, 속도가
(3)
위 두 식에서 t를 소거하면
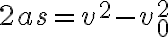
위 두 식에서 t를 소거하면
etc ¶
힘,force(F)와 일,work(W)의 관계:
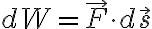
퍼텐셜에너지,potential_energy(U)와 일,work(W)의 관계:
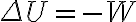 이것들은 전위 공부하다 온 건데.....맞나?
이것들은 전위 공부하다 온 건데.....맞나?
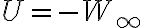 <- 무슨뜻?
<- 무슨뜻?
최단시간강하곡선문제,brachistochrone problem
Brachistochrone curve (곡선,curve)
브라키스토크론
단어 뜻: shortest time
 최단시간강하곡선
최단시간강하곡선
 Brachistochrone
Brachistochrone
http://mathworld.wolfram.com/BrachistochroneProblem.html
![[https]](/123/imgs/https.png) 수학백과: 최속강하곡선
수학백과: 최속강하곡선
 최단시간강하곡선_문제(Brachistochrone_problem)
최단시간강하곡선_문제(Brachistochrone_problem)
Brachistochrone curve (곡선,curve)
브라키스토크론
단어 뜻: shortest time
http://mathworld.wolfram.com/BrachistochroneProblem.html
![[https]](/123/imgs/https.png) 수학백과: 최속강하곡선
수학백과: 최속강하곡선등시곡선
 Tautochrone_curve AKA isochrone curve
Tautochrone_curve AKA isochrone curve
(tauto- = same, iso- = equal, chrono = time)
이것도 cycloid. 뒤집은.
Huygens가 tautochrone problem의 정답이 cycloid임을 밝힘.
관련글: https://ghebook.blogspot.com/2020/12/tautochrone-curve.html
![[https]](/123/imgs/https.png) 수학백과: 등시곡선
수학백과: 등시곡선
 등시강하곡선_문제_(Tautochrone_problem)
등시강하곡선_문제_(Tautochrone_problem)
(tauto- = same, iso- = equal, chrono = time)
이것도 cycloid. 뒤집은.
Huygens가 tautochrone problem의 정답이 cycloid임을 밝힘.
관련글: https://ghebook.blogspot.com/2020/12/tautochrone-curve.html
![[https]](/123/imgs/https.png) 수학백과: 등시곡선
수학백과: 등시곡선Structure and Interpretation of Classical Mechanics (mit.edu)
https://mitpress.mit.edu/sites/default/files/titles/content/sicm_edition_2/book.html
https://news.ycombinator.com/item?id=23153778
Scheme 사용
https://mitpress.mit.edu/sites/default/files/titles/content/sicm_edition_2/book.html
https://news.ycombinator.com/item?id=23153778
Scheme 사용

