전속밀도(electric flux density) 또는 전기변위장(electric displacment field), 변위장, electric displacement
그냥 전기장,electric_field ) 는 진공에 대해 정의되었는데 유전체,dielectric 등의 편극성(편극,polarization) 물질에서는 외부 전기장에 의해 분극이 일어나므로 .. 암튼 물질에 대한 효과까지 고려한 장이 전기변위장인가 보다.
는 진공에 대해 정의되었는데 유전체,dielectric 등의 편극성(편극,polarization) 물질에서는 외부 전기장에 의해 분극이 일어나므로 .. 암튼 물질에 대한 효과까지 고려한 장이 전기변위장인가 보다.
맞다. 그리고 그 관계는 재료,material의 유전율,permittivity ε에 관련되며
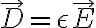
의 관계를 가지며, 유전율 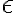 은
은

이고, 여기서
 : electrical permittivity of free space (F/m)
: electrical permittivity of free space (F/m)
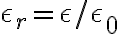 : relative permittivity (or 유전상수,dielectric_constant) of the material
: relative permittivity (or 유전상수,dielectric_constant) of the material
이것의 자기장 버전이 자기장세기,magnetic_field_intensity 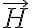 란다.
란다.
from https://namu.wiki/w/전기 변위장 CHK
맞다. 그리고 그 관계는 재료,material의 유전율,permittivity ε에 관련되며
from https://namu.wiki/w/전기 변위장 CHK
CLEANUP ¶
{
변위장 D, 전기장 E, 편극밀도,polarization_density P

