기호: 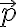
정의: 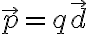
단위: C·m
from parent page; merge: {
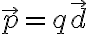
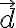 : 음의 전하로부터 양의 전하에 이르는 변위벡터,displacement_vector
: 음의 전하로부터 양의 전하에 이르는 변위벡터,displacement_vector
}
q:방향이 그렇게 정의된 이유는?
즉, 전하량이 크고, 서로 떨어진 거리가 멀면 쌍극자모멘트가 크다.전기장 E 안의 쌍극자의 전기쌍극자모멘트 ¶
관련된듯? http://www.kocw.net/home/search/kemView.do?kemId=433549 1. 전기현상 가우스 법칙 26:40
{
전하 -q, +q로 구성된 전기쌍극자,electric_dipole가 있고
-q까지 가는 벡터가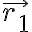 (위치벡터,position_vector)
(위치벡터,position_vector)
+q까지 가는 벡터가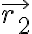
-q에 가해지는 힘은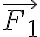
+q에 가해지는 힘은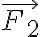
-q에서 +q로 가는 변위가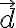
일 때
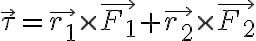
+\vec{r_2}\times(+q\vec{E}))
\times\vec{E})
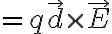
따라서
{
전하 -q, +q로 구성된 전기쌍극자,electric_dipole가 있고
-q까지 가는 벡터가
+q까지 가는 벡터가
-q에 가해지는 힘은
+q에 가해지는 힘은
-q에서 +q로 가는 변위가
일 때
}
퍼텐셜에너지,potential_energy 관련 ¶
Twins
전기 쌍극자 모멘트(electric dipole moment)
https://ghebook.blogspot.kr/2011/09/electric-dipole-moment.html
한글자료, 내용은 어려움
https://ghebook.blogspot.kr/2011/09/electric-dipole-moment.html
한글자료, 내용은 어려움


![[https]](/123/imgs/https.png)