전하량은 같고 부호,sign가 반대인 두 전하,electric_charge가 일정한 거리,distance만큼 떨어져 있을 때 이 두 전하의 분포를 전기 쌍극자라고 한다. (+)에서 나가고 (-)로 들어가는 전기장,electric_field을 형성한다. (하이탑 물II)
크기가 같고 부호가 반대인 두 점전하가 짧은 거리(d)만큼 떨어져 덩어리를 이루고 있는 것
two charges of equal strength
opposite polarity
separated by a small distance
opposite polarity
separated by a small distance
d는 -q에서 +q로 가는 변위,displacement? CHK
전기장 식 유도
(+)와 (-)전하가 각각 끼치는 영향을 생각.
}=\frac1{4\pi\varepsilon_0}\frac{q}{r_{(+)})
}=\frac1{4\pi\varepsilon_0}\frac{q}{r_{(-)})
}-E_{(-)})
^2}-\frac1{(z+d/2)^2} \right))
^2})
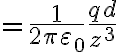
슬라이드에는
}-E_{(-)})

(최준곤)
같은 magnitude의, 반대 부호의, 전하 q를 가진 두 입자
사이 거리가 d
사이 거리가 d
z거리에 ...
Up: 쌍극자,dipole
----


![[https]](/123/imgs/https.png)