AKA direct comparison test
양수일때만 가능. 이유 추가 tbw
모든  에 대하여
에 대하여 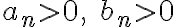 일 때
일 때
 이 수렴하고
이 수렴하고 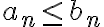 이면
이면 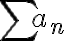 도 수렴한다.
도 수렴한다.
 이 발산하고
이 발산하고 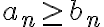 이면
이면 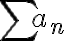 도 발산한다.
도 발산한다.
i)
정리 2.4: 비교 검사
두 급수 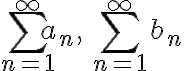 가
가
충분히 큰 모든 에 대해
에 대해  을 만족하고,
을 만족하고,
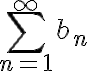 이 수렴하면
이 수렴하면 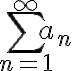 역시 수렴한다.
역시 수렴한다.
여기서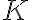 는 영보다 큰 상수이다.
는 영보다 큰 상수이다.
충분히 큰 모든
여기서
한편 충분히 큰 모든  에 대해
에 대해 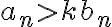 을 만족하고,
을 만족하고,
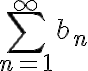 이 발산하면
이 발산하면 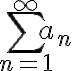 역시 발산한다.
역시 발산한다.
여기서 는 영보다 큰 상수이다.
는 영보다 큰 상수이다.
여기서
(이승준 p24)
Ex ¶
Ex.

Sol.
앞의 몇 개는 상관이 없고
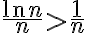 for
for 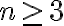 and
and 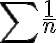 is div.
is div.
by comparison test, divergent.
앞의 몇 개는 상관이 없고
by comparison test, divergent.
Compare: 극한비교판정법,limit_comparison_test
Twins:
![[https]](/123/imgs/https.png) 수학백과: 비교판정법
수학백과: 비교판정법
{ merge to 본문
비교할 대상이 되는 다른 급수가 있어야 한다. 당연히...
여기엔 주로 p급수,p-series, 등비급수(기하급수,geometric_series)같이 수렴/발산 여부가 알려진 것을 (- 쉽게 알/판정할 수 있는 것을??) 사용...
}
 비교판정법
비교판정법
 Direct_comparison_test
Direct_comparison_test
![[https]](/123/imgs/https.png) 수학백과: 비교판정법
수학백과: 비교판정법{ merge to 본문
비교할 대상이 되는 다른 급수가 있어야 한다. 당연히...
여기엔 주로 p급수,p-series, 등비급수(기하급수,geometric_series)같이 수렴/발산 여부가 알려진 것을 (- 쉽게 알/판정할 수 있는 것을??) 사용...
}

