기하급수,geometric_series(=등비급수)는
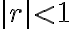 이면 수렴
이면 수렴
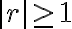 이면 발산
이면 발산
Sub:
일반항판정법 = n항판정법 = 발산판정법 - 가장 기본, 밑에 1.1. 참조
비교판정법,comparison_test
극한비교판정법,limit_comparison_test
적분판정법,integral_test
비율판정법,ratio_test
근판정법,root_test
교대급수판정법,alternating_series_test
p급수 판정법 - p급수,p-series
바이어슈트라스_M-판정법,Weierstrass_M-test - writing; tmp see 바이어슈트라스 판정법
바이어슈트라스 판정법
디리클레_판정법,Dirichlet_test - writing; 디리클레 판정법
디리클레 판정법
아벨_판정법,Abel_test - writing; 아벨 판정법
아벨 판정법
Cauchy_test or Cauchy_convergence_test - writing; cauchy convergence test ... rel. 코시_수열,Cauchy_sequence
cauchy convergence test ... rel. 코시_수열,Cauchy_sequence
코시_응집판정법,Cauchy_condensation_test - writing; cauchy condensation test
cauchy condensation test
비교판정법,comparison_test
극한비교판정법,limit_comparison_test
적분판정법,integral_test
비율판정법,ratio_test
근판정법,root_test
교대급수판정법,alternating_series_test
p급수 판정법 - p급수,p-series
바이어슈트라스_M-판정법,Weierstrass_M-test - writing; tmp see
디리클레_판정법,Dirichlet_test - writing;
아벨_판정법,Abel_test - writing;
Cauchy_test or Cauchy_convergence_test - writing;
코시_응집판정법,Cauchy_condensation_test - writing;
1.1. 발산 판정법 ¶
1.2. 절대수렴 (and 조건수렴) ¶
만약 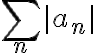 이 수렴한다면
이 수렴한다면  또한 수렴한다.
또한 수렴한다.
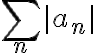 이 수렴하면 급수
이 수렴하면 급수  은 '절대수렴'한다고 말한다.
은 '절대수렴'한다고 말한다.
 은 수렴하지만
은 수렴하지만 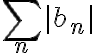 은 발산하면 급수
은 발산하면 급수  은 '조건수렴'한다고 말한다.
은 '조건수렴'한다고 말한다.
1.5. p>1이면 p-급수는 수렴 ¶
p급수,p-series 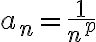 의 수렴 조건은 적분판정법을 통해 얻을 수 있다.
의 수렴 조건은 적분판정법을 통해 얻을 수 있다.
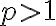 이면 급수
이면 급수 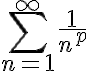 은 수렴하고,
은 수렴하고,
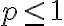 이면 발산한다.
이면 발산한다.
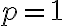 은 발산하는 조화급수,harmonic_series
은 발산하는 조화급수,harmonic_series 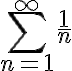 에 해당한다는 점을 주의하라.
에 해당한다는 점을 주의하라.
1.6. 직접 비교 판정법 ¶
때때로 급수  의 수렴 특성은, 수렴 특성이 알려진 다른 급수
의 수렴 특성은, 수렴 특성이 알려진 다른 급수  과의 비교를 통해 이해될 수 있다. 한 가지 방법은 각 항의 값을 직접 비교하는 것이다. 이를 통해 다음과 같은 결론을 도출할 수 있다.
과의 비교를 통해 이해될 수 있다. 한 가지 방법은 각 항의 값을 직접 비교하는 것이다. 이를 통해 다음과 같은 결론을 도출할 수 있다.
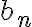 이 항상
이 항상 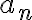 보다 크고,
보다 크고,  이 수렴하기 때문에
이 수렴하기 때문에  도 수렴해야 한다.
도 수렴해야 한다.
두 번째 결론은 이 논리를 역으로 사용한다.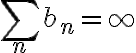 이고
이고 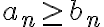 이기 때문에 또한
이기 때문에 또한  이어야 한다.
이어야 한다.
- 만약 모든
에 대해
이고,
이 수렴하면,
도 수렴한다.
- 만약 모든
에 대해
이고,
이 발산하면,
도 발산한다.
두 번째 결론은 이 논리를 역으로 사용한다.
1.7. 극한 비교 판정법 ¶
- 만약
이면
과
은 모두 수렴하거나 모두 발산한다.
- 만약
이고
이 수렴하면
도 수렴한다.
- 만약
이고
이 발산하면
도 발산한다.
1.9. 비율 판정법 ¶
가장 유용한 수렴 판정법. 수열에서 이어지는 항들의 비율의 극한을 계산한다.
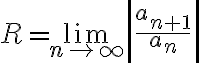
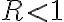 이면 급수
이면 급수  은 수렴하고,
은 수렴하고,
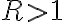 이면
이면  은 발산한다.
은 발산한다.
만약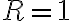 이면, 이 판정법은 결정적이지 않다.
이면, 이 판정법은 결정적이지 않다.
만약
3. 판정법의 요약 ¶
일반항 판정법:
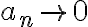 이 아니면, 급수는 발산한다.
이 아니면, 급수는 발산한다.
기하급수,geometric_series:
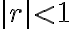 이면
이면 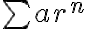 은 수렴한다.
은 수렴한다.
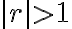 이면 급수는 발산한다.
이면 급수는 발산한다.
p급수,p-series:
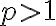 이면
이면 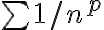 은 수렴한다. 그렇지 않으면 발산한다.
은 수렴한다. 그렇지 않으면 발산한다.
음수항을 갖지 않는 급수:
교대급수:
(Thomas 13e ko chap8.6(교대급수와 조건수렴)의 마지막 box)
적분판정법,integral_test, 비판정법(비율판정법,ratio_test), 근판정법,root_test을 사용한다. 수렴여부를 아는 급수와 비교하는 비교판정법,comparison_test 또는 극한비교판정법,limit_comparison_test을 사용한다.
음수항을 갖는 급수:교대급수:
(Thomas 13e ko chap8.6(교대급수와 조건수렴)의 마지막 box)
5. links ko ¶
해석학의 여러가지 급수판정법 총정리
Series convergence test
https://freshrimpsushi.github.io/posts/series-convergence-test/
Series convergence test
https://freshrimpsushi.github.io/posts/series-convergence-test/

