임의의 실수 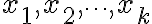 와
와 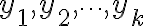 에 대해 다음이 성립.
에 대해 다음이 성립.
^2\le(x_1^2+x_2^2+\cdots+x_k^2)(y_1^2+y_2^2+\cdots+y_k^2))
pf.
\cdot(tA+B))
)+B\cdot(tA+B))
+A\cdot B)+B\cdot(tA)+B\cdot B)
+2t(A\cdot B)+B\cdot B)
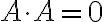 인 경우, 부등식이 성립
인 경우, 부등식이 성립
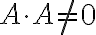 인 경우, t에 대한 2차식인데 이게 항상 0 이상이므로, 판별식을 생각하면 부등식이 성립
인 경우, t에 대한 2차식인데 이게 항상 0 이상이므로, 판별식을 생각하면 부등식이 성립
함수에 대한 C-S 부등식은 함수공간,function_space#s-1 밑부분도 참조.
Twins:
![[https]](/123/imgs/https.png) Namu: 코시-슈바르츠 부등식
Namu: 코시-슈바르츠 부등식
![[https]](/123/imgs/https.png) 수학백과: 코시-슈바르츠 부등식
수학백과: 코시-슈바르츠 부등식
 코시-슈바르츠_부등식
코시-슈바르츠_부등식
 Cauchy–Schwarz_inequality
Cauchy–Schwarz_inequality
https://encyclopediaofmath.org/wiki/Cauchy_Schwarz_inequality
https://mathworld.wolfram.com/CauchysInequality.html
https://mathworld.wolfram.com/SchwarzsInequality.html
https://everything2.com/title/Cauchy-Schwarz inequality
![[https]](/123/imgs/https.png) Namu: 코시-슈바르츠 부등식
Namu: 코시-슈바르츠 부등식![[https]](/123/imgs/https.png) 수학백과: 코시-슈바르츠 부등식
수학백과: 코시-슈바르츠 부등식https://encyclopediaofmath.org/wiki/Cauchy_Schwarz_inequality
https://mathworld.wolfram.com/CauchysInequality.html
https://mathworld.wolfram.com/SchwarzsInequality.html
https://everything2.com/title/Cauchy-Schwarz inequality

