Related: 절대값,absolute_value과 관련이 깊다.
사전 지식:
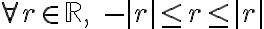
Proof 1 ¶
먼저 알아두어야 할 것.
* Let r>0, then |x|<r ⇔ -r<x<r
* a가 실수이고 r이 양의 실수일 때, 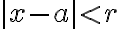 ⇔ a-r < x < a+r
⇔ a-r < x < a+r
따라서 둘을 더하면,
여기서
Proof 2 ¶
먼저 필요한 지식:
양수 A, B에 대해,
A²>B² iff A²-B²>0 iff (A+B)(A-B)>0 iff A-B>0 iff A>B
ab≥0일 때는 위의 식은 0이 되고,
ab<0일 때는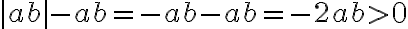 따라서 위의 식은 양수가 된다. (등호는 ab≥0일 때)
따라서 위의 식은 양수가 된다. (등호는 ab≥0일 때)
ab<0일 때는
Proof 3 ¶
한줄로 요약하면
^2 = x^2+2xy+y^2 \le |x|^2+2|x||y|+|y|^2 = (|x|+|y|)^2)
먼저 증명해야 할 theorem은,
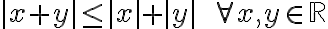
양변을 제곱하면,
^2)
이것을 보이는 것이 목적이다.
증명.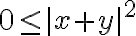 ……(1)
……(1)
^2)
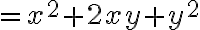
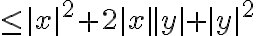
^2) ……(2)
……(2)
위에서 (1)과 (2)를 비교하면
증명.
∴ 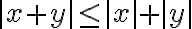
Proof 6 ¶
사전지식
^2)
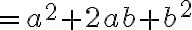
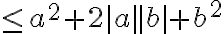

^2)
따라서 위 중간의 부등호를 생각해 시작과 끝 식으로 정리하면
^2)
그리고 0 이상의 실수 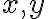 에 대해,
에 대해, 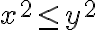 이면
이면 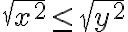 이므로
이므로 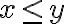 이다.
이다. 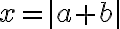 그리고
그리고 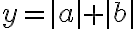 라 하면 바로 위 부등식에서부터
라 하면 바로 위 부등식에서부터
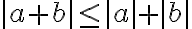
(Thomas 11e 연습문제 1.45)
또는
이다. 그래서 제곱하면
rel ¶
mklink
코시-슈바르츠_부등식,Cauchy-Schwartz_inequality
민코프스키_부등식,Minkowski_inequality - 작성중
삼각형,triangle
거리공간,metric_space - see libre
코시-슈바르츠_부등식,Cauchy-Schwartz_inequality
민코프스키_부등식,Minkowski_inequality - 작성중
삼각형,triangle
거리공간,metric_space - see libre
tmp links ¶
todo ¶
수의 삼각부등식과 벡터의 삼각부등식을 나중에 분리.
QQQ 대충, (특히 벡터의) 삼각부등식은 '돌아가는 경로보다 직선경로가 더 짧다' 는 그런 것인데 ...  Fermat_principle 변분법,variational_calculus 최소화,minimization , ... , 두 점,point을 사이의 shortest_path 가 직선,line이라는 것, ... 과 유사한데 정확한 관계가?
Fermat_principle 변분법,variational_calculus 최소화,minimization , ... , 두 점,point을 사이의 shortest_path 가 직선,line이라는 것, ... 과 유사한데 정확한 관계가?
Twins:
https://mathworld.wolfram.com/TriangleInequality.html
https://proofwiki.org/wiki/Triangle_Inequality
 Triangle_inequality
Triangle_inequality
 삼각_부등식
삼각_부등식
https://ncatlab.org/nlab/show/triangle inequality
https://everything2.com/title/triangle inequality
 삼각부등식
삼각부등식
https://planetmath.org/triangleinequality
https://planetmath.org/triangleinequalityofcomplexnumbers (복소수,complex_number인 경우의 증명)
https://mathworld.wolfram.com/TriangleInequality.html
https://proofwiki.org/wiki/Triangle_Inequality
https://ncatlab.org/nlab/show/triangle inequality
https://everything2.com/title/triangle inequality
https://planetmath.org/triangleinequality
https://planetmath.org/triangleinequalityofcomplexnumbers (복소수,complex_number인 경우의 증명)
Up: 부등식,inequality


![[http]](/123/imgs/http.png)