If  has a local maximum or minimum at
has a local maximum or minimum at 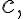
and if) exits,
exits,
then=0.)
and if
then
(Proof)  가
가 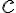 에서 극대라 가정하면,
에서 극대라 가정하면,  가
가 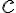 에 충분히 가까울 때
에 충분히 가까울 때 \ge f(x)) 이다. 이것이 암시하는 것은
이다. 이것이 암시하는 것은 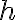 가 0에 충분히 가까울 때 (
가 0에 충분히 가까울 때 ( 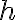 의 부호는 무관 )
의 부호는 무관 )
\ge f(c+h))
따라서
-f(c)\le 0)
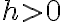 인 경우. 양변을 작은 양수
인 경우. 양변을 작은 양수 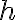 로 나누면
로 나누면
-f(c)}{h}\le 0)
양쪽의 우극한right-hand_limit을 취하면
-f(c)}{h}\le\lim_{h\to 0^+}0=0)
) 이므로
이므로
=\lim_{h\to 0}\frac{f(c+h)-f(c)}{h}=\lim_{h\to 0^+}\frac{f(c+h)-f(c)}{h})
따라서
\le 0)
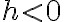 인 경우,
인 경우,
-f(c)}{h}\ge 0)
양쪽의 좌극한left-hand_limit을 취하면
=\lim_{h\to 0}\frac{f(c+h)-f(c)}{h}=\lim_{h\to 0^-}\frac{f(c+h)-f(c)}{h}\ge 0)
이상 \ge 0) 그리고
그리고 \le 0) 둘 다 참임을 보였으므로 반드시
둘 다 참임을 보였으므로 반드시 =0) 이다.
이다.
이상 극대의 경우의 증명이며 극소의 경우도 비슷한 방식으로 증명한다.
(Stewart)
AKA 페르마의 임계점 정리, 임계점 정리[1]
----
- [1] 페르마의 임계점 정리에 의하면 “열린 구간에서 정의된 미분 가능한 함수 f(x)의 극점(extreme_point? extremal_point? extremum? PAGENAME TBD. rel. 극값,extremum
 극점 )에서는 순간변화율이 영이다.” (김홍종 미적 1+ p393, 부록 수학사전 - 임계점 정리)
극점 )에서는 순간변화율이 영이다.” (김홍종 미적 1+ p393, 부록 수학사전 - 임계점 정리)

