표준편차,standard_deviation

표준편차,standard_deviation (rev. 1.37)
표기:
σ, SD, STD, s, etc.

고딩레벨에선 항상 분산,variance의 제곱근인듯?
$\sigma=\sqrt{V}$
$\sigma_x=\sqrt{V_x}$
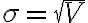
$\sigma(x)=\sqrt{V(x)}$

표준편차(STD)는 분산(VAR)의 양의 제곱근
$STD(X)=\sigma_X:=\sqrt{VAR(X)}$

모표준편차,population_standard_deviation σ
{
모평균,population_mean μ를 가지고 계산
}
표본표준편차,sample_standard_deviation s
{
표본평균,sample_mean X̅를 가지고 계산
}

모표준편차: 데이터 수 $N$ 으로 나눔.
$\sigma=\sqrt{\frac{\textstyle\sum(x_i-\mu)^2}{N}}$
표본표준편차: 표본 자료 수보다 작은 $n-1$ 로 나눔.
$s_x=\sqrt{\frac{\textstyle\sum(x_i-\bar{x})^2}{n-1}}$
//tmp expr from [https]khan


[edit]

성질

$VAR(aX+b)=a^2VAR(X)$
$STD(aX+b)=|a|STD(X)$

pf. $V[aX+b]$
$=E[(aX+b-E(aX+b))^2]$
$=E[(aX+b-(aE(X)+b))^2]$
$=E[(aX+b-aE(X)-b)^2]$
$=E[(aX-aE(X))^2]$
$=E[a^2(X-(E(X))^2]$
$=a^2E[X-(E(X))^2]$
$=a^2V[X]$

[edit]

tmp

분산,variance 뿐만 아니라 표준편차도 있는 이유는, 분산은 제곱하여 나온 것이기 때문에 실제 scale? 단위? 차원?... 와 동떨어질 수 있어서.

근데 표준편차 역시 문제점이 있는데
(여러 집합/집단 의 표준편차를 비교한다는 전제...)
표준편차는 퍼져있는 정도를 알아보자는 건데,
data 집합 크기(?? 확실히)에 따라 ....(대충 scale이 제각각이라는 얘기)
그래서 이 문제를 해결하기 위해 '표준편차'보다 '평균을 고려한 표준편차'개념이 만들어졌고
이것을 변동계수,variation_coefficient라 한다.

http://www.kocw.net/home/search/kemView.do?kemId=1162312 2장. 자료의 표현_변동성 에 의하면.. begin


이것들은 산포도,dispersion의 측도,measure이고,

표준편차 SD는 제곱평균제곱근,root_mean_square,RMS로 나타내는데
$SD=\sqrt{\frac1{n}\sum_{i=1}^{n}(x_i-\bar{x})^2}$
CHK

표본표준편차,sample_standard_deviation (s)
$s=\sqrt{\frac1{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2}$
n을 n-1로만 바꾼 것.

n-1: 자유롭게 가질 수 있는 편차의 개수 - 자유도,degree_of_freedom라고 함

표본분산,sample_variance (s2)
표본분산은 표본표준편차의 제곱.
$s^2=\frac1{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2$

표본분산의 간편식:
$s^2=\frac1{n-1}\left(\sum_{i=1}^{n}x_i^2-n(\bar{x})^2\right)=\frac1{n(n-1)}\left(n\sum_{i=1}^{n}x_i^2-\left(\sum_{i=1}^{n}x_i\right)^2\right)$



end TOCLEANUP

표본분산 간이식(from kocw [http]숙대 강의자료3 p106)
$s^2=\frac1{n-1}\sum(x_i-\bar{x})^2=\frac1{n-1}\left(\sum x_i^2-n\bar{x}^2\right)=\frac1{n-1}\left(\sum x_i^2-\frac1{n}\left(\sum x_i\right)^2\right)$



표준오차,standard_error와 다르다. 비교해 적을 것. TBW

이름이 편차,deviation이므로 평균과의 차이를 나타내는 것이 맞는지 chk