편차,deviation

$i$ 번째 표본의 편차는
$x_i-\bar{x}$
즉 자료값(변량,variance)과 평균,mean,average의 차이,difference.

편차 = 변량 - 평균

편차의 합은 0.

그냥 편차가 위 식과 같을 때,
절대편차: absolute deviation - 편차의 절대값
$|x_i-\bar{x}|$
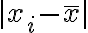
제곱편차: 편차의 제곱
$(x_i-\bar{x})^2$

평균편차 mean deviation AKA deviation from the mean

평균절대편차 mean absolute deviation, MAD / average absolute deviation, AAD
{
절대편차의 평균 = 평균 절대편차

WpKo:평균_절대_편차에서 다음을 모두 묶어 언급. 완전히 동일?
평균 편차(mean deviation)
절대 편차(absolute deviation)
평균 절대 편차(average absolute deviation 또는 mean absolute deviation, AAD, MAD)

see also:
https://hsm-edu.tistory.com/758?category=810686 4)

[https]수학백과: 평균 절대편차 - 간단히 평균편차라고 하기도
}

중앙값절대편차 median absolute deviation, MAD
중앙값,median

최소절대편차 least absolute deviation, LAD
회귀분석,regression_analysis에 사용 (curr see 회귀,regression)

사분위편차 quartile deviation
사분위편차,quartile_deviation
mklink 사분위수,quartile 사분범위,interquartile_range,IQR
... Naver:사분위편차 Google:사분위편차 Google:quartile deviation

표준편차 standard deviation, SD
표준편차,standard_deviation
모표준편차,population_standard_deviation
표본표준편차,sample_standard_deviation

평균제곱편차 mean squared deviation MSD = 평균제곱오차,mean_square_error,MSE


(tmp)
절대편차,absolute_deviation
{
절대편차
absolute deviation

Ndict:절대편차
Ggl:absolute deviation
} // absolute deviation
평균편차,mean_deviation
{
평균편차
mean deviation

Ndict:평균편차
Ggl:mean deviation
} // mean deviation

비슷? : 오차,error, 잔차,residual
[https]수학백과를 읽고 나중에 정리예정 TODO

산포도,dispersion와 관련성 TBW
그냥 개개의 '편차'는 dimension(?)이 다르고. 편차를 전체적으로 본 것(ex. 표준편차, 평균절대편차 etc.)는 산포도를 나타내는 지표.

분산,variance 계산에 필요.

[edit]

tmp from 수학백과 편차

산포도,dispersion를 보기 위해서는
  • 절대편차의 평균(=평균 절대편차)
  • 제곱편차의 평균(=분산)
  • 분산의 제곱근(=표준편차)
등이 많이 쓰인다.