자유도,degree_of_freedom

기호: df, dof

주로 통계학, 물리학(강체역학), 기계공학(기구학), 화학(분자운동 - 분자,molecule의 진동,oscillation,vibration 등, 각종 입자,particle의 운동,motion.)에서 언급되는 개념.

좌표,coordinate, 차원,dimension과도 관련있는데 구체적으로 어떤지 서술.
{
// 2021-12-23 chk
동역학계,dynamical system의 자유도의 수는 그것의 위상공간,phase_space의 차원,dimension. 다시 말해 modeler가 그 계,system를 완벅하게 기술하기 위해 필요하다고 느끼는 변수,variable의 수.
Hamiltonian_systems 맥락에서, 자유도의 수는 상태변수,state_variable의 ,pairs의 수,number.[1]
}

보통 '주어진 (제한/구속)조건(제약,constraint 조건,condition, 제약조건, ...아마 '한계(limit, limitation)'나 '경계,bound'와 비슷?)' 내에서/하에서 얼마나 변화할 수 있는가?? - chk

기계 관련하여 축,axis, 접합부(joint), ...
통계에선 모집단,population과 표본,sample간의 관계에서 통계적 추정,estimation과 관련있음.

[edit]

통계 관련

예를 들어 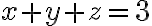$x+y+z=3$ 이라는 방정식이 있다면, 얼핏 보면 독립변수,independent_variable 개수가 3개인 것 같지만 아니다. 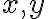$x,y$ 가 정해지면 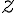$z$ 가 유일하게 정해질 수 밖에 없기 때문에 이 때 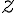$z$ 는 종속변수,dependent_variable가 되고 독립변수는 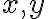$x,y$ 두 개다. (마찬가지로 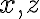$x,z$ 가 정해지면 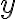$y$ 가 유일하게 정해질 수 밖에 없고, etc.) 그래서 이 식의 자유도는 2가 된다.

t분포,t-distribution와 카이제곱분포,chi-squared_distribution가 특히 자주 같이 언급되는데 어떤 관련인지 chk
t-분포 발견자 Student(Gosset)이 자유도의 발견자임. t-분포와 함께 자유도가 발견?
개념을 최초로 발견한 것은 Gauss, 정교하게 발전시킨 것은 Gosset, 용어 명명자는 Fisher(1922).

t분포, χ²분포, F분포,F-distribution 이것들이 밀접한데 mklink

다음에선 $n$ 이 아닌 $n-1$ 로 나누는 것이 언급됨. 자유도 관련하여.
표본분산,sample_variance
표본표준편차,sample_standard_deviation

[edit]

tmp bmks en


// 위에서 연결된건데 ME관련.
https://everything2.com/title/six degrees of freedom

// 위에서 연결된건데 graph_theory 관련. link, node, traveling, small world, .. 여기부터는 이 페이지와 무관. degree 페이지가 생기면 옮길것. or del ok.
https://everything2.com/title/Six Degrees of Everything
https://everything2.com/title/Six Degrees of Separation - 케빈 베이컨, 에르되시 수 WpKo:에르되시_수, ... small-world_network or small_world_network 그거.
rel.
WpEn:Six_Degrees_of_Kevin_Bacon Namu:6단계 법칙 에르되시_수,Erdos_number(writing)


----