그린 정리는 스토크스_정리,Stokes_theorem의 특수한 경우임.
Stewart ¶
그린 정리는 단순닫힌곡선 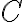 를 따른 선적분,line_integral과 // 단순닫힌곡선 = simply_closed_curve ? ... 단순곡선,simple_curve 닫힌곡선,closed_curve
를 따른 선적분,line_integral과 // 단순닫힌곡선 = simply_closed_curve ? ... 단순곡선,simple_curve 닫힌곡선,closed_curve
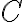 로 둘러싸인 평면영역
로 둘러싸인 평면영역  에서의 이중적분,double_integral 사이의 관계를 알려준다.
에서의 이중적분,double_integral 사이의 관계를 알려준다.
(정리)
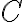 는 평면에 놓은 양의 방향을 갖는 조각마다 매끄러운 단순닫힌곡선이라 하고,
는 평면에 놓은 양의 방향을 갖는 조각마다 매끄러운 단순닫힌곡선이라 하고,
 는
는 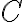 로 둘러싸인 영역이라 하자.
로 둘러싸인 영역이라 하자.
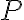 와
와  가
가  를 포함하는 열린영역,open_region에서 연속인 편도함수를 가지면, 다음이 성립한다.
를 포함하는 열린영역,open_region에서 연속인 편도함수를 가지면, 다음이 성립한다.
dA)
 의 양의 방향인 경계곡선에 대한 또 다른 기호는
의 양의 방향인 경계곡선에 대한 또 다른 기호는 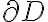 이다. 따라서 식을 다음과 같이 쓸 수 있다.
이다. 따라서 식을 다음과 같이 쓸 수 있다.
dA = \int_{\partial D}P\,dx + Q\,dy)
(Stewart 8e ko p914)
Zill ¶
(Zill 6e ko chap9.12 p681)
위의 것은 평면 형태, 이후 Stokes 정리 앞부분(p697)에서 3차원 공간의 Green 정리 언급.
위의 것은 평면 형태, 이후 Stokes 정리 앞부분(p697)에서 3차원 공간의 Green 정리 언급.
Bazett ¶
Green's Theorem (Circulation-Curl Form)
 dxdy)
For 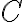 smooth, simple, closed curve enclosing
smooth, simple, closed curve enclosing 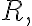
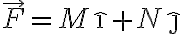 having
having 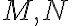 having continuous first partials in an open region containing
having continuous first partials in an open region containing 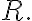
좌변은 ccw circulation.
우변의 괄호 안은 circulation_density.
우변의 괄호 안은 circulation_density.
관련: 순환,circulation
{
관련: 회전,rotation 회전,curl 순환,cycle 순환순열/순환순서/etc. (related: 순열,permutation mentioned in: 레비치비타_기호,Levi-Civita_symbol)
}
{
관련: 회전,rotation 회전,curl 순환,cycle 순환순열/순환순서/etc. (related: 순열,permutation mentioned in: 레비치비타_기호,Levi-Civita_symbol)
}
O'Neil ¶
Let 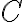 be a simple closed positively oriented path in the plane.
be a simple closed positively oriented path in the plane.
Let consist of all points on
consist of all points on 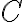 and in its interior. Let
and in its interior. Let
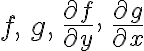
be continuous on 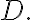 Then:
Then:
dx+g(x,y)dy=\iint_D \left(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\right) dA)
(O'Neil AEM 7e, Thm 12.1)
Let


![[https]](/123/imgs/https.png)