curl(vector_field_in) = ∇×(vector_field_in) = (vector_field_out)

항상??

벡터장,vector_field을 벡터장으로 만드는 연산자.
벡터장의 curl이 설명하는 것: 그것의 rotational property 또는 circulation. // 회전,rotation 순환,circulation

벡터곱,vector_product,cross_product으로 정의되므로 3차원 벡터장,vector_field에서만 정의.
$\vec{v}:\mathbb{R}^3\to\mathbb{R}^3$
$(v_x(x,y,z),v_y(x,y,z),v_z(x,y,z))$
$\operatorname{curl}\vec{v}=\nabla\times\vec{v}=\left(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z},\,\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x},\,\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\right)$

표기 형식:

∇ × (벡터장)
i.e.
(델,del,나블라,nabla) (벡터곱,vector_product,cross_product 연산자) (벡터장)

$\nabla\times\vec{F}=\begin{vmatrix}\hat{x}&\hat{y}&\hat{z}\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\F_x&F_y&F_z\end{vmatrix}$

$=\hat{x}\left(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}\right)-\hat{y}\left(\frac{\partial F_z}{\partial x}-\frac{\partial F_x}{\partial z}\right)+\hat{z}\left(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right)$

(정의)
벡터장,vector_field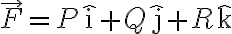 $\vec{F}=P\hat{\rm i}+Q\hat{\rm j}+R\hat{\rm k}$ 의 회전(curl)은 벡터장

$\operatorname{curl}\vec{F}=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\hat{\rm i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\hat{\rm j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\hat{\rm k}$

이다.
실제로(actually의 번역인듯? '사실') curl F는 델 연산자와 벡터 F의 외적,outer_product으로 계산할 수 있다.

$\operatorname{curl}\vec{F}=\nabla\times\vec{F}=\begin{vmatrix}\hat{\rm i}&\hat{\rm j}&\hat{\rm k}\\\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\P&Q&R\end{vmatrix}$

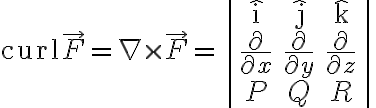
(Zill 6e ko p637 정의 9.7.1 회전)

[edit]

Vector identities involving the curl / 성질 ¶

임의의 벡터 $\vec{a},\vec{b}$ 와 스칼라 V에 대해
⑴ $\nabla\times(\vec{a}+\vec{b})=\nabla\times\vec{a}+\nabla\times\vec{b}$
⑵ $\nabla\cdot(\nabla\times\vec{a})=0$
⑶ $\nabla\times(\nabla V)=0$
(Ulaby 7e p166 3.106a-c)

벡터장의 회전 연산(curl operation)은
분배법칙이 성립함,
교환법칙과 결합법칙은 성립하지 않음.

i.e. $A,B$ 가 미분가능한 벡터장이라면

$\nabla\times(A+B)=\nabla\times A + \nabla\times B$
$\nabla\times A \ne A\times\nabla$
$\nabla\times(A\times B) \ne (\nabla\times A)\times B$

from https://blog.naver.com/mykepzzang/221357195753

[edit]

벡터장의 회전이 0이면 ¶

스토크스_정리,Stokes_theorem 참조.
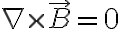벡터장 $\vec{B}$ 에서 $\nabla\times\vec{B}=0$ 이면, 그 벡터장은 conservative or irrotational하다고 한다. Because its circulation(회전,curl 참조), represented by the RHS of (Stokes' Thm), is zero, irrespective of the contour chosen.
(Ulaby 7e p166 3-6.2 Stokes' Thm)

[edit]

tmp from 전기전자공부방 ¶

$\vec{A}$ 의 회전은 축(회전축)벡터로, (?)
그 크기는 면적이 0으로 줄어들 때 단위면적당 $\vec{A}$ 의 최대 순환을 의미하고,
방향은 최대 회전을 만드는 면의 법선 방향

link

벡터의 회전

직교좌표계에서

$\vec{A}=\langle A_x,A_y,A_z \rangle=A_x\hat{x}+A_y\hat{y}+A_z\hat{z}$

$\nabla\times\vec{A}=\begin{vmatrix}\hat{x}&\hat{y}&\hat{z}\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\A_x&A_y&A_z\end{vmatrix}$
$=\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}\right)\hat{x}-(...)\hat{y}+(...)\hat{z}$

원통좌표계에서

$\vec{A}=\langle A_{\rho},A_{\phi}, A_z \rangle=A_{\rho}\hat{\rho} + A_{\phi}\hat{\phi} + A_z\hat{z}$

$\nabla\times\vec{A}=\frac1{\rho}\begin{vmatrix}\hat{\rho}&\hat{\phi}&\hat{z}\\ \frac{\partial}{\partial\rho}&\frac{\partial}{\partial\phi}&\frac{\partial}{\partial z}\\ A_{\rho}&\rho A_{\phi}&A_z\end{vmatrix}$
$=\hat{\rho}\left( \frac{\partial A_z}{\partial\phi} - \frac{\partial}{\partial z}\rho A_{\phi}\right)\cdot\frac{1}{\rho} - \rho\hat{\phi}\left( \frac{\partial A_z}{\partial \rho}-\frac{\partial A_{\rho}}{\partial z} \right)\cdot\frac1{\rho} + \hat{z}\left(\frac{\partial\rho A_{\phi}}{\partial\rho}-\frac{\partial A_{\rho}}{\partial\phi}\right)\cdot\frac{1}{\rho}$

계수 $\frac1\rho$ 가 붙고 두번째 항에 $\rho$ 가 붙음을 주의
두번째 항은 rho가 cancel되네?

구좌표계

$\vec{A}=\langle A_r,A_\theta,A_\phi \rangle=A_r\hat{r}+A_\theta\hat{\theta}+A_\phi\hat{\phi}$

$\nabla\times\vec{A}=\frac{1}{r^2\sin\theta}\begin{vmatrix}\hat{r}&r\hat{\theta}&r\sin\theta\hat{\phi}\\ \frac{\partial}{\partial r}&\frac{\partial}{\partial\theta} & \frac{\partial}{\partial\phi} \\ A_r & rA_{\theta} & r\sin\theta A_{\phi} \end{vmatrix}$