표면  를 포함하는 영역에서 주어진 벡터장
를 포함하는 영역에서 주어진 벡터장  가 매끄러운 표면
가 매끄러운 표면  를 포함하는 영역에서 연속일 때,
를 포함하는 영역에서 연속일 때,  를 통한
를 통한  의 면적분 또는 선속은
의 면적분 또는 선속은
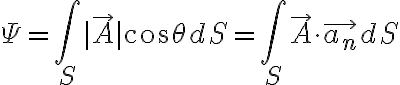
또는 간단하게
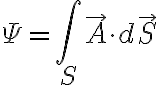
으로 정의한다.
폐곡면(어떤 체적을 정의하는)의 경우 위 식은
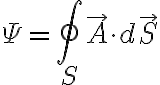
가 되며, 이것은  를 통해 밖으로 나가는 A의 순 선속이라 한다.
를 통해 밖으로 나가는 A의 순 선속이라 한다.
여기서
 : 표면이므로 분명 곡면,surface
: 표면이므로 분명 곡면,surface
 : 벡터장,vector_field
: 벡터장,vector_field
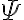 : 선속,flux
: 선속,flux
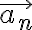 : 면
: 면  상의 임의의 점에서
상의 임의의 점에서  에 대한 단위법선벡터(see 단위벡터,unit_vector and 법선벡터,normal_vector)
에 대한 단위법선벡터(see 단위벡터,unit_vector and 법선벡터,normal_vector)
(Sadiku 3.3)
면벡터란 법선벡터(normal vector)의 일종인 면법선벡터(surface normal vector)를 뜻하는 듯. 면에 수직인 벡터. (방향은?) CHK
2020-09-16 from 차동우: 스토크스 정리와 다이버젠스 정리 https://youtu.be/Sa7xDuWEvZ4 9:40 CHK
2020-09-16 from 차동우: 스토크스 정리와 다이버젠스 정리 https://youtu.be/Sa7xDuWEvZ4 9:40 CHK
면벡터의 방향은 바깥쪽 (이건 그냥 관례, 약속인 듯. x축이 오른쪽 방향인 것 처럼.)
The definition of the surface area of S:
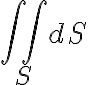
밀도,density 사용한 예:
xy평면에 놓인 얇은 면에서, 면적밀도(area density, mass per unit area)가 x와 y에 따라 변하고, 이 면의 전체 질량을 구한다고 하자.
면을 면적밀도가 거의 비슷한(approximately constant) 미세한 2차원 조각(segment)으로 나눠야 한다.
각 조각의 면적밀도가 σi이고 면적이 dAi이면 각 조각의 질량은 σi dAi
더하면 면의 질량은
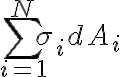
더 정확하게 하기 위해, 조각을 작게 하는 극한을 취하면, 즉 dA가 0으로, N이 무한으로 가면 합은 적분이 되므로 질량은
 dA)
이것은 면 S 위에서 스칼라함수 σ(x,y)의 area integral이다.
xy평면에 놓인 얇은 면에서, 면적밀도(area density, mass per unit area)가 x와 y에 따라 변하고, 이 면의 전체 질량을 구한다고 하자.
면을 면적밀도가 거의 비슷한(approximately constant) 미세한 2차원 조각(segment)으로 나눠야 한다.
각 조각의 면적밀도가 σi이고 면적이 dAi이면 각 조각의 질량은 σi dAi
더하면 면의 질량은
(Fleisch 2008)
Compare: area_integral
not in kms; 넓이적분?
넓이,area 적분,integration
https://mathworld.wolfram.com/AreaIntegral.html
{ 내용 짧으므로 그대로 적으면,
A 이중적분,double_integral over 3 coord.s giving the 넓이,area within some 영역,region
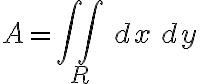
If a 평면곡선,plane_curve is given by ,)
then the area between the curve and the x-axis from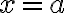 to
to 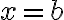 is given by
is given by
dx)
}
not in kms; 넓이적분?
넓이,area 적분,integration
https://mathworld.wolfram.com/AreaIntegral.html
{ 내용 짧으므로 그대로 적으면,
A 이중적분,double_integral over 3 coord.s giving the 넓이,area within some 영역,region
then the area between the curve and the x-axis from
Related: 면적분이 활용되는/나오는 곳
스토크스_정리,Stokes_theorem
가우스_법칙,Gauss_s_law
앙페르_법칙,Ampere_s_law
발산정리,divergence_theorem는 ....6개 면에 대한 면적분이 결국 이 부피체에 의한 삼중적분의 값과 같다는 것.... DELME TMP CHK - curr. goto 발산,divergence
선속,flux
가우스_법칙,Gauss_s_law
앙페르_법칙,Ampere_s_law
발산정리,divergence_theorem는 ....6개 면에 대한 면적분이 결국 이 부피체에 의한 삼중적분의 값과 같다는 것.... DELME TMP CHK - curr. goto 발산,divergence
선속,flux
AKA 곡면적분, 면적적분
Compare: 선적분,line_integral


![[https]](/123/imgs/https.png)