//from http://www.kocw.net/home/search/kemView.do?kemId=1162312 5장_표본분포_중심극한의정리
확률변수,random_variable들 X1, …, Xn 들이 독립이고 정규분포,normal_distribution N(μ, σ2)에 따른다면,
중심극한정리
X1, …, Xn : 독립, 유한평균 μ, 유한분산 σ2을 갖는 동일한 분포 →
확률변수,random_variable들 X1, …, Xn 들이 독립이고 정규분포,normal_distribution N(μ, σ2)에 따른다면,
중심극한정리
X1, …, Xn : 독립, 유한평균 μ, 유한분산 σ2을 갖는 동일한 분포 →
n이 커짐에 따라, )
Let \quad(i=1,\cdots,n)) : i.i.d (서로 독립)
: i.i.d (서로 독립)
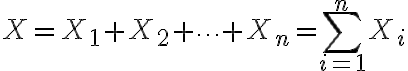 :
:
}{n}\right))
이항분포 B(n,p), 평균 μ=np, 분산 σ2=np(1-p)
By CLT,표본,sample 표본평균,sample_mean 정규분포,normal_distribution 근사,approximation 적률생성함수,moment_generating_function,MGF
모집단,population에서 뽑은 표본,sample이 충분히 크다면, 표본평균,sample_mean의 분포는 정규분포,normal_distribution에 근사한다는 것
from/see http://blog.naver.com/mykepzzang/220851280035
모집단,population에서 뽑은 표본,sample이 충분히 크다면, 표본평균,sample_mean의 분포는 정규분포,normal_distribution에 근사한다는 것
from/see http://blog.naver.com/mykepzzang/220851280035
Related ¶
CLT와 ICA(독립성분분석,independent_component_analysis,ICA)은 반대 개념이라고... (see 주성분분석,principal_component_analysis,PCA)


![[https]](/123/imgs/https.png)