AKA 가우스 분포, 가우시안 분포, Gaussian distribution
확률밀도함수,probability_density_function,PDF는
(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-m)^2}{2\sigma^2}})
그 성질은
=\frac1{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}})
그 그래프가 종형을 닮아서 bell curve라고 함. (다만 정규분포가 아닌 것 중에서도 bell shaped curve가 있음.)
{
-σ to σ : 68%
-2σ to 2σ : 95%
-3σ to 3σ : 99.7%
- x=m에 대해 좌우 대칭
- x=m일 때 최대
- x축이 점근선
- 곡선과 x축 사이의 넓이는 1
{
-σ to σ : 68%
-2σ to 2σ : 95%
-3σ to 3σ : 99.7%
i.e.
=0.6826)
=0.9544)
=0.9974)
}
}
표준화. 표준정규분포.
Sub: 정규분포 중에서 평균=0, 표준편차=1인 것을 표준정규분포,standard_normal_distribution이라고 한다.
확률변수 가 정규분포를 따를 때,
가 정규분포를 따를 때,
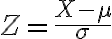
로 변환하면 확률변수 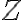 는 표준정규분포
는 표준정규분포 ) 을 따른다.
을 따른다.
확률변수 ) 에 대한 표준화 변수는
에 대한 표준화 변수는 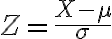
i.e.확률변수
이항분포와의 관련성 서술.
이항분포,binomial_distribution에서 시행의 횟수가 많아지면 정규분포에 가까워진다는 것 서술. n이 커질 때 B(n,p)는 N(np, npq)로 간다는 .... CHK
중심극한정리,central_limit_theorem,CLT는 확률분포,probability_distribution를 알 수 없는 어떠한 변수(확률변수,random_variable?)라도 정해진 횟수  만큼 독립적으로 추출하는 작업을 반복했을 때, 추출된 값들의 평균값은
만큼 독립적으로 추출하는 작업을 반복했을 때, 추출된 값들의 평균값은  이 커짐에 따라 정규분포에 접근한다는 정리.[1]
이 커짐에 따라 정규분포에 접근한다는 정리.[1]
{
표본평균,sample_mean의 확률분포,probability_distribution는 정규분포에 수렴한다. 모집단,population 확률변수의 분포가 정규분포가 아니어도, 표본의 크기가 대략 30개 이상이면 표본평균의 확률분포는 정규분포를 보인다. ...CHK
{
표본평균,sample_mean의 확률분포,probability_distribution는 정규분포에 수렴한다. 모집단,population 확률변수의 분포가 정규분포가 아니어도, 표본의 크기가 대략 30개 이상이면 표본평균의 확률분포는 정규분포를 보인다. ...CHK
tmp from https://bookdown.org/mathemedicine/Stat_book/normal-distribution.html
 이 커지면, 특히 30 이상이 되면, 표본평균,sample_mean
이 커지면, 특히 30 이상이 되면, 표본평균,sample_mean 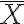 는 평균이
는 평균이 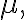 분산이
분산이 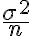 인 정규분포
인 정규분포 ) 을 따를 것 같은데,
을 따를 것 같은데,
....중략....
평균이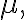 분산이
분산이 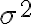 인 모집단,population(정규분포일 필요 없음)에서,
인 모집단,population(정규분포일 필요 없음)에서,  개의 표본,sample을 뽑아서 계산한 표본평균,sample_mean
개의 표본,sample을 뽑아서 계산한 표본평균,sample_mean 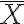 는
는  이 커질 때
이 커질 때 ) 을 따른다. 이것이 바로 CLT. CHK
을 따른다. 이것이 바로 CLT. CHK
}
....중략....
평균이
}
저런 복잡한 수식이 나오는 이유는  De_Moivre–Laplace_theorem https://mathworld.wolfram.com/deMoivre-LaplaceTheorem.html 참조.
De_Moivre–Laplace_theorem https://mathworld.wolfram.com/deMoivre-LaplaceTheorem.html 참조.
드무아브르-라플라스 정리는 중심극한정리,central_limit_theorem,CLT의 특수한 경우이다. 이 정리는 정규분포가 특정 조건 아래서 이항분포,binomial_distribution에 대한 근사,approximation로 쓰일 수 있음을 보여준다.
푸아송_분포,Poisson_distribution는 큰 값에 대해 이항분포에 대한 또 다른 방식의 근사이다. (wpen)
값에 대해 이항분포에 대한 또 다른 방식의 근사이다. (wpen)
푸아송_분포,Poisson_distribution는 큰
tmp links ko ¶
https://jinseob2kim.github.io/Normal_distribution.html
이항분포,binomial_distribution, 그 근사/일반화를 통한 정규분포 접근, 오차,error의 법칙, 중심극한정리,central_limit_theorem,CLT 순으로 언급됨.
이항분포,binomial_distribution, 그 근사/일반화를 통한 정규분포 접근, 오차,error의 법칙, 중심극한정리,central_limit_theorem,CLT 순으로 언급됨.
주의: 정규분포는 standard distribution이 아님. NORMAL DISTRIBUTION임.
![[https]](/123/imgs/https.png) 물리학백과: 정규분포 Gaussian distribution 가우스분포
물리학백과: 정규분포 Gaussian distribution 가우스분포
https://everything2.com/title/Gaussian Distribution
 Normal_distribution
Normal_distribution
 정규_분포
정규_분포
 Normal_distribution
Normal_distribution
https://en.citizendium.org/wiki/Normal_distribution
표준정규분포는 standard normal distribution.
Twins:![[https]](/123/imgs/https.png) 물리학백과: 정규분포 Gaussian distribution 가우스분포
물리학백과: 정규분포 Gaussian distribution 가우스분포https://everything2.com/title/Gaussian Distribution
https://en.citizendium.org/wiki/Normal_distribution
----
- [1] 물리학백과: 정규분포 앞부분

