감마함수,gamma_function

Difference between r1.44 and the current

@@ -35,6 +35,14 @@
[[베타분포,beta_distribution]]

}
= Euler's reflection formula =
Euler_reflection_formula
$\Gamma(z)\Gamma(1-z) = \frac{\pi}{\sin(\pi z)},\;\;\; z\not\in\mathbb{Z}$
MKL: [[Leonhard_Euler]]? [[반사,reflection]]
Ggl:"Euler's reflection formula"

= Bmks =
ALSOIN [[리만_제타함수,Riemann_zeta_function]]:
@@ -54,7 +62,6 @@

Up: [[수학,math]]/[[함수,function]]
해석적확장 해석적연속 analytic_continuation - 의 좋은 예 중의 하나가 감마함수.




$$\mathrm{\Gamma}(x)=\int_{0}^{\infty}t^{x-1}e^{-t}dt=\int_{0}^{\infty}e^{-t}t^{x-1}dt$$
$\Re(x)>0$ 에서만?

$\mathrm{\Gamma}(x+1)=x\mathrm{\Gamma}(x),\quad\quad x>0$

계승,factorial과의 관계:
$\mathrm{\Gamma}(x)=(x-1)!$
$\mathrm{\Gamma}(n+1)=n!$
chk - 감마함수는 계승,factorial을 복소수,complex_number 범위로 일반화,generalization한 게 맞는지
ie 계승의 정의역을 자연수,natural_number에서 확장한것인지..
근데 1만큼 차이나는데 저것을 잠시 멈추고 생각하지 않고 바로바로 나오는 방법??

기타 신기한 성질:
$\mathrm{\Gamma}\left(\frac12\right)=\sqrt{\pi}$


베타 함수 $B(a,b)$ 는 다음과 같이 정의한다.
$B(a,b)\equiv\int_0^1 x^{a-1} (1-x)^{b-1} \,dx$
위의 정의에 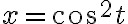$x=\cos^2 t$ 의 치환을 적용하면 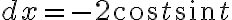$dx=-2\cos t\sin t$ 이므로 다음을 얻는데,
$B(a,b)=2\int_0^{\pi/2} \cos^{2a-1} t \, \sin^{2b-1} t \,dt$
이 식은 위 식 대신에 베타 함수의 정의로 사용되기도 한다.

(중략)

베타 함수와 감마함수,gamma_function의 관계식은
$B(a,b)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$

(이승준 p61-62)


}

[edit]

Euler's reflection formula

[edit]

Bmks

ALSOIN 리만_제타함수,Riemann_zeta_function:
[https]네이버캐스트: 리만가설 이야기 - 리만제타함수, 감마함수, 그 관계 언급. 저기 [https]세번째 글 제목이 감마 함수이나, 전체를 순서대로 보는 게 좋음.

[edit]

Twins: Ref: