5.4. using gamma function ¶
순열의 경우,
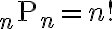
sub?
상승계승 rising_factorial
하강계승 falling_factorial
/// 상승계승
상승계승  rising.factorial
rising.factorial  falling.factorial
falling.factorial
상승계승 rising_factorial
하강계승 falling_factorial
///
계승은 자연수,natural_number ℕ0에서 정의.
계승을 더 (정의역,domain을 자연수→실수 확장,extension?? 일반화,generalization? chk) 일반적으로 확장시킨 개념은 감마함수,gamma_function를 참조.
참고로,
)
계승의 다양한 확장
https://jjycjnmath.tistory.com/515
Bhargava_factorial
{
Bhargava factorial
 Bhargava_factorial
Bhargava_factorial
"Bhargava factorial"
 Bhargava factorial
Bhargava factorial
}
계승을 더 (정의역,domain을 자연수→실수 확장,extension?? 일반화,generalization? chk) 일반적으로 확장시킨 개념은 감마함수,gamma_function를 참조.
참고로,
https://jjycjnmath.tistory.com/515
- 감마함수
- 준계승(subfactorial) - 완전순열 complete_permutation or 교란 derangement 관련, (curr see 순열,permutation) (derangement : see
 Derangement)
Derangement)
- 이중계승(double factorial) 및 다중계승(multiple factorial, multifactorial)
- 소수계승(primorial)
- 초계승(superfactorial)
Bhargava_factorial
{
Bhargava factorial
"Bhargava factorial"
}
AKA 팩토리얼, 차례곱(북한말)
CHK 한자 이름 階乘에서 계는 단계/계단 할 때 그거?[1]
----
- [1] "계승이란 단계를 내려가듯이 숫자를 하나씩 줄여가면서 곱해가는 연산을 말한다." (통계가 빨라지는 수학력)


![[https]](/123/imgs/https.png)