리만_제타함수,Riemann_zeta_function

기호 ζ

ζ(x) = 1 + 2−x + 3−x + 4−x + ⋯

$\zeta(x)=\sum_{n=1}^{\infty}\frac1{n^x}$

$\zeta(s)=\frac1{1^s}+\frac1{2^s}+\frac1{3^s}+\frac1{4^s}+\frac1{5^s}+\cdots$

$\zeta(s)=\sum_{n=1}^{\infty}n^{-s}$


ζ(1)인 경우는 조화급수,harmonic_series의 일종.
관련: p급수,p-series

Euler Product Formula
$\zeta(s)=\sum_{n}\frac{1}{n^s}=\prod_{p}\frac1{1-p^{-s}}$
n, p는 양수이고 p는 소수,prime_number

// tmp via https://mathphysics.tistory.com/703 '리만제타함수의 기본성질' slide
{
오일러_곱,Euler_product? ...곱,product

Euler product:
$\zeta(s)=\prod_p \frac1{1-p^{-s}} \;\; (\operatorname{Re}(s)>1)$
그럼 저 위에 Re(s)>1 ...조건 필요?

chk.
}
제타함수,zeta_function의 정의역을 복소수로 확장한 것이 리만의 제타함수.
이것의 일반화로 Hurwitz_zeta_function ..






zeta fn.


tmp
https://everything2.com/title/Riemann zeta function
{
//LionMan
infinite_sum 으로 처음 정의
$\operatorname{Zeta}(n):=\sum_{m=0}^{\infty} \frac1{m^n}$
복소평면,complex_plane으로 해석적 확장하면 (analytically extended)
$\operatorname{Zeta}(z):=\frac{\int_{0}^{\infty}\frac{u^{z-1}}{e^u-1}du}{\Gamma(z)}$
$\operatorname{Zeta}(z):=\frac{\textstyle\int_{0}^{\infty}\frac{u^{z-1}}{e^u-1}du}{\Gamma(z)}$

//abiessu
오일러가 증명하길
$\operatorname{Zeta}(z):=\sum_{m=0}^{\infty}\frac1{m^z}$
는 다음과 같다. 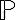$\mathbb{P}$ 는 소수,prime_number.
$\prod_{p\in\mathbb{P}}\frac1{1-p^{-z}}$
다시 말해 다음과 같다.
$\frac1{1-2^{-z}} \cdot \frac1{1-3^{-z}} \cdot \frac1{1-5^{-z}} \cdot \frac1{1-7^{-z}} \cdot \cdots$
....tbw
}