귀류법,proof_by_contradiction

reductio ad absurdum (Latin)
歸(돌아올 귀) 謬(그릇될 류) 法

주장이 거짓,false이라고 가정,assumption한 뒤 모순,contradiction된 결과가 유도됨을 보여 주장이 참,true임을 보이는 증명,proof법.

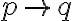AKA 모순증명법. 조건문 WtEn:conditional_statement？ x (2023-11) WpEn:Conditional_statement？ Ndict:조건문 $p\to q$ 를 증명,proof할 때, 가정,assumption 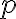$p$ 가 참,true이고 결론,conclusion 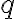$q$ 가 거짓,false이라고 가정,assumption하여 모순,contradiction이 생김을 보여서 증명을 완성하는 기법. 직접적으로 증명할 수 없는 경우에 유용한 간접증명법이다.[1]


[edit]

merge; from 논리,logic

{


쉬운 예
AKA
reductio ad absurdum, RAA (Latin) 불합리로의 회귀, 터무니 없는 것으로 돌아가기
배리법
반증법
}

[edit]

Ex 1

$\sqrt{2}$ 가 무리수임을 증명

$\left(\frac{a}{b}\right)^2=2$ 를 만족하는 양의 정수 $a,b$ 가 있다고 가정한다. 양변에 $b^2$ 을 곱하면,
$a^2=2b^2\quad\quad(a^2>b^2>0)$
따라서 $a^2$ 은 짝수이다. 그런데 $a^2$ 이 짝수이면 $a$ 도 짝수이다. (홀수의 제곱은 홀수, 짝수의 제곱은 짝수) 따라서 새로운 양의 정수 $c$ 를 도입하여 $a=2c$ 라고 하고 대입하면,
$4c^2=2b^2$
양변을 2로 나누면,
$b^2=2c^2\quad\quad(b^2>c^2>0)$
이와 같이 반복하면 얻어지는 관계는 다음과 같다.
$a^2=2b^2,\;b^2=2c^2,\;c^2=2d^2,\;d^2=2e^2,\;\ldots$
$a^2>b^2>c^2>d^2>e^2>\ldots$
어떤 양의 짝수를 계속해서 2로 나누다 보면 더는 나눌 수 없는 시점이 찾아오기 마련이다. 그러나 위 방법은 $a$ 와 $b$ 를 2로 무한 번 나눌 수 있다는 주장을 하므로, 처음부터 가정이 잘못되었다.
따라서 제곱해서 2가 되는 유리수는 존재하지 않는다.

(실체에 이르는 길 1)

[edit]

Misc

(Joke) 모든 수,number는 interesting number라는 것의 증명
가정,assumption: 수는 정수,integer이고 모든 정수를 interesting vs uninteresting number로 (구분하는 기준criterion이 존재하여) 이분,bipartition할 수 있다면?
https://everything2.com/title/interesting number

TBW 배중률,law_of_excluded_middle(curr goto 논리,logic)과 분명히 밀접한데 구체적 연관 서술
{
2023-01-10
대충

아리스토텔레스,Aristotle 이후의 논리적 원리는 배중률에 기초하지만
위상수학자 Brouwer { WpKo:라위천_에흐베르튀스_얀_브라우어르 WpEn:L._E._J._Brouwer } 의 직관주의,intuitionism는 배중률을 배척??

수학의 많은 존재 증명(존재성,existence 증명,proof)은 '존재하지 않는다면 모순,contradiction이 유도된다'는 (가정,assumption?) 귀류법,proof_by_contradiction에 의존하지만, Brouwer의 직관주의에 따르면, 존재하지 않으면 모순이 생긴다는 것이 존재한다는 것으로 귀결될 이유가 없다. - 존재증명에는 더 구체적인 뭔가가 더 필요하다?


}


----