AKA 논리학
Sub:
오류,error와의 차이는?![[https]](/123/imgs/https.png) 두산백과는 실질적 오류(error)와 논리적 오류(fallacy)로 구분.
두산백과는 실질적 오류(error)와 논리적 오류(fallacy)로 구분.
형식적 오류 formal fallacy w
비형식적 오류 informal fallacy w
mathematical fallacy ... mathematical fallacy
mathematical fallacy
일차논리,first-order_logic (= 술어논리,predicate_logic)
불_논리,Boolean_logic - 불_대수,Boolean_algebra와 같은건가? 차이가 있다면? QQQ
명제논리,propositional_logic (= 영차논리,zeroth-order_logic)
술어논리,predicate_logic
퍼지논리,fuzzy_logic - 작성중
logic_programming - 작성중
logical_derivation - derivation - https://encyclopediaofmath.org/wiki/Derivation,_logical
논리적오류,logical_fallacy 논리오류? ... 오류,fallacy? pagename TBD
{불_논리,Boolean_logic - 불_대수,Boolean_algebra와 같은건가? 차이가 있다면? QQQ
= 이치논리? 두값논리?
다치논리? 여러값논리? many-valued_logic { https://encyclopediaofmath.org/wiki/Many-valued_logic }명제논리,propositional_logic (= 영차논리,zeroth-order_logic)
술어논리,predicate_logic
퍼지논리,fuzzy_logic - 작성중
logic_programming - 작성중
logical_derivation - derivation - https://encyclopediaofmath.org/wiki/Derivation,_logical
논리적오류,logical_fallacy 논리오류? ... 오류,fallacy? pagename TBD
오류,error와의 차이는?
![[https]](/123/imgs/https.png) 두산백과는 실질적 오류(error)와 논리적 오류(fallacy)로 구분.
두산백과는 실질적 오류(error)와 논리적 오류(fallacy)로 구분.- error : 판단이 대응하는 사물과 일치하지 않는 것
- fallacy : 사고 법칙에서 어긋난 것
형식적 오류 formal fallacy w
비형식적 오류 informal fallacy w
mathematical fallacy ...
TBW 이것들간의 관계 명확히
{
수리논리 수리논리,mathematical_logic
명제논리 명제논리,propositional_logic - 명제,proposition = 명제proposition
명제proposition
술어논리 술어논리,predicate_logic - 술어 서술어 술부 predicate
형식논리,formal_logic
등 각종 논리 추가및 관계서술
{
수리논리 수리논리,mathematical_logic
명제논리 명제논리,propositional_logic - 명제,proposition =
술어논리 술어논리,predicate_logic - 술어 서술어 술부 predicate
형식논리,formal_logic
등 각종 논리 추가및 관계서술
//2021-07-20 가대 황병언 http://www.kocw.net/home/search/kemView.do?kemId=1395260 2. 5:30
명제논리 vs 술어논리:
명제,proposition논리, 술어,predicate논리:
주어와 술어를 구별하는 지 여부로.
명제논리 vs 술어논리:
명제,proposition논리, 술어,predicate논리:
주어와 술어를 구별하는 지 여부로.
명제논리
주어와 술어를 구분하지 않고 전체를 하나의 식으로 처리하여 (참 또는 거짓)을 판별하는 법칙
술어논리주어와 술어로 구별하여 참 또는 거짓에 대한 법칙(sic)
}1. 함의 implication ¶
어떤 명제에 대한 검증.
수학적 세계를 구성하는 추상적 대상에 관한 특정한 형태의 주장.
각 함의는 형식적으로 세 부분으로 되어 있음.
즉 "p는 q를 함의한다"는 기호로 p⇒q.
수학적 세계를 구성하는 추상적 대상에 관한 특정한 형태의 주장.
각 함의는 형식적으로 세 부분으로 되어 있음.
즉 "p는 q를 함의한다"는 기호로 p⇒q.
Summary. p⇒q에 쓸 수 있는 용어들은
- p는 q를 함의한다.
- 만일 p이면 q이다.
- q는 p에서 추론된다.
- p는 q가 되기 위한 충분조건이다.
- q는 p가 되기 위한 필요조건이다.
2. tmp from Varberg Calcu. A Bit of Logic ¶
이건너무쉽지만 영어용어복습으로...DELME
Law of excluded middle: either R or ~R, but not both.
| Symbol | Statement |
| P⇒Q | If P then Q; P implies Q (P=hypothesis, Q=conclusion) |
| Q⇒P | converse of P⇒Q |
| ~P | negation of P |
| ~Q⇒~P | contrapositive of P⇒Q |
Law of excluded middle: either R or ~R, but not both.
3. tmp - order로 분류하는 logics? ¶
from https://zariski.wordpress.com/2019/04/29/deephol-딥러닝을-이용한-수학-명제-자동증명-시스템/
영차논리 : 변수없이 참/거짓을 판정하는 서술, = 명제 논리(propositional logic)
일차논리 : 술부에 quantifier로 한정된 변수를 쓰는 것이 허용가능한 논리, 괴델의 완전성 정리가 성립 (see 일차논리,first-order_logic)
이차논리 : Second-order_logic괴델의 불완전성 정리가 성립
Second-order_logic괴델의 불완전성 정리가 성립
고차논리 : Higher-order_logic
Higher-order_logic
영차논리 : 변수없이 참/거짓을 판정하는 서술, = 명제 논리(propositional logic)
일차논리 : 술부에 quantifier로 한정된 변수를 쓰는 것이 허용가능한 논리, 괴델의 완전성 정리가 성립 (see 일차논리,first-order_logic)
이차논리 :
고차논리 :
// from https://ncatlab.org/nlab/show/predicate logic
logic
logic
0th-order logic = 영차논리,zeroth-order_logic = 명제논리,propositional_logic
1st-order logic = 일차논리,first-order_logic = 술어논리,predicate_logic
2nd-order logic = 이차논리,second-order_logic
higher-order logic = 고차논리,higher-order_logic
Related: 영차집합론? zeroth-order_set_theory - https://ncatlab.org/nlab/show/zeroth-order set theory - 집합론,set_theory1st-order logic = 일차논리,first-order_logic = 술어논리,predicate_logic
2nd-order logic = 이차논리,second-order_logic
higher-order logic = 고차논리,higher-order_logic
영차논리,zeroth-order_logic - writing
일차논리,first-order_logic (= 술어논리,predicate_logic)
이차논리,second-order_logic
고차논리,higher-order_logic
일차논리,first-order_logic (= 술어논리,predicate_logic)
이차논리,second-order_logic
고차논리,higher-order_logic
4. tmp 여러 logic ¶
배중률,law_of_excluded_middle공리가 고전논리에서는 중요시 됨. 이것이 없으면 직관논리 / 직관주의 / 직관주의논리 / intuitionistic_logic
Twins:
https://pub.mearie.org/고전논리
 고전_논리
고전_논리
 Classical_logic
Classical_logic
https://ncatlab.org/nlab/show/classical logic
https://pub.mearie.org/고전논리
https://ncatlab.org/nlab/show/classical logic
직관논리
직관적논리?
rel. 직관,intuition
 직관_논리
직관_논리
 Intuitionistic_logic (더 일반적인 constructive logic으로 불리기도 한다고 - constructive logic(구성논리? 구성적논리?)이 intui..(직관논리)보다 더 일반적인 단어라는 뜻인가? 그렇다면 이유는?)
Intuitionistic_logic (더 일반적인 constructive logic으로 불리기도 한다고 - constructive logic(구성논리? 구성적논리?)이 intui..(직관논리)보다 더 일반적인 단어라는 뜻인가? 그렇다면 이유는?)
직관적논리?
rel. 직관,intuition
Hilbert's program, 메타수학,metamathematics 관련 - see  Metamathematics https://everything2.com/title/metamathematics (del)
Metamathematics https://everything2.com/title/metamathematics (del)
https://ncatlab.org/nlab/show/intuitionistic logicparaconsistent_logic - 초일관논리? - writing
minimal_logic or minimal_calculus
{
 Minimal_logic (minimal calculus) - a symbolic logic system
Minimal_logic (minimal calculus) - a symbolic logic system
https://ncatlab.org/nlab/show/minimal logic
}
{
https://ncatlab.org/nlab/show/minimal logic
}
Twins:
![[https]](/123/imgs/https.png) 교육학용어사전: 양상논리학
교육학용어사전: 양상논리학
![[https]](/123/imgs/https.png) 두산백과: 양상 논리
두산백과: 양상 논리
 Modal_logic
Modal_logic
 양상_논리
양상_논리
https://ncatlab.org/nlab/show/modal logic
https://encyclopediaofmath.org/wiki/Modal_logic
https://plato.stanford.edu/entries/logic-modal/
 양상논리
양상논리
https://everything2.com/title/Modal Logic
}
![[https]](/123/imgs/https.png) 교육학용어사전: 양상논리학
교육학용어사전: 양상논리학![[https]](/123/imgs/https.png) 두산백과: 양상 논리
두산백과: 양상 논리https://ncatlab.org/nlab/show/modal logic
https://encyclopediaofmath.org/wiki/Modal_logic
https://plato.stanford.edu/entries/logic-modal/
https://everything2.com/title/Modal Logic
}
5. 단어 / 표현 / topics ¶
logical_consequence
{
// from 02logical-consequence-theory.pdf
정의:
 논리적_귀결 - aka entailment, - 관련표현: 그러므로, therefore, ∴, ⊨(
논리적_귀결 - aka entailment, - 관련표현: 그러므로, therefore, ∴, ⊨( 이중_턴스틸,
이중_턴스틸,  Double_turnstile), entails
Double_turnstile), entails
 Logical_consequence
Logical_consequence
}
술어,predicate
soundness and completeness - 건전성,soundness { 건전성
건전성  Soundness } 과 완전성,completeness
Soundness } 과 완전성,completeness
명제,proposition
p->q에서 p는 가정, q는 결론
역,converse // conversion
이,inverse
대우,contraposition // contrapositive Q: 이건?![[https]](/123/imgs/https.png) https://en.wikipedia.org/wiki/Transposition_(logic)
https://en.wikipedia.org/wiki/Transposition_(logic)
p→q에 대해,
내포,implication ⇒ // imply
추론
연역,deduction
귀납,induction (유도,induction와 같은 단어)
배중률,law_of_excluded_middle - writing
{
// from 02logical-consequence-theory.pdf
정의:
U : a set of formulas
A : a formula
일 때,
A is a logical consequence of U, denoted U ⊨ A, iff every model of U is a model of A.
A : a formula
일 때,
A is a logical consequence of U, denoted U ⊨ A, iff every model of U is a model of A.
찾아보니 ⊨말고⊧ and ∴말고⛬ 나오는데 이건 뭐지?
}
술어,predicate
soundness and completeness - 건전성,soundness {
명제,proposition
statement은?
관계,relationp->q에서 p는 가정, q는 결론
역,converse // conversion
이,inverse
대우,contraposition // contrapositive Q: 이건?
![[https]](/123/imgs/https.png) https://en.wikipedia.org/wiki/Transposition_(logic)
https://en.wikipedia.org/wiki/Transposition_(logic)p→q에 대해,
| 역 | q→p |
| 이 | ~p→~q |
| 대우 | ~q→~p |
추론
연역,deduction
귀납,induction (유도,induction와 같은 단어)
배중률,law_of_excluded_middle - writing
이분법,dichotomy
resolution - http://foldoc.org/resolution 의 2. 를 참조.
6. logical operations ¶
| ¬ negation 부정 | not | 부정,negation |
| ∧ conjunction 논리곱 | and | 논리곱,conjunction |
| ∨ disjunction 논리합 | or | 논리합,disjunction |
| ⇒ conditional | if…then | 조건부,conditional?? |
| ⇔ biconditional 쌍조건문, 겹조건문 | if and only if, iff | |
ISO 문서에서. from https://people.engr.ncsu.edu/jwilson/files/mathsigns.pdf
| ¬p | negation of p | not p |
| p∧q | conjunction of p and q | p and q |
| p∨q | disjunction of p and q | p or q |
| p⇒q | p implies q, if p then q | implication ... pagename tbd, 함의,implication 함축,implication 암시,implication 내포,implication 임플리케이션,implication |
| p⇔q | p is equivalent to q | 동치,equivalence? |
7. quantifiers 한정기호 ¶
∀ universal quantifier: "for every x", "for all x"
∃ existential quantifier: "there exists an x such that"
∃1, ∃! unique existential quantifier
∃ existential quantifier: "there exists an x such that"
∃1, ∃! unique existential quantifier
kms의 번역용어:
quantifier 한정기호
existential quantifier 존재기호
universal quantifier 전칭기호, 보편기호
quantifier 한정기호
existential quantifier 존재기호
universal quantifier 전칭기호, 보편기호
8. de_Morgan_s_law ¶
\bigwedge
\bigvee
)
)
\bigcap \bigcup
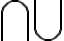
\bigvee
\bigcap \bigcup
참조한 자료:
Introduction to Higher Mathematics, by Patrick Keef and David Guichard
https://www.whitman.edu/mathematics/higher_math_online
Introduction to Higher Mathematics, by Patrick Keef and David Guichard
https://www.whitman.edu/mathematics/higher_math_online

