급수,series에서 나머지 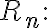
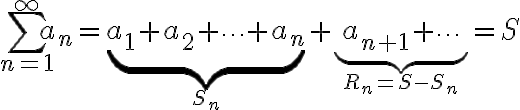
이 때 나머지의 범위는
dx \le R_n \le \int_n^{\infty}f(x)dx)
(이것이 왜 그런지는 =a_n) 과 적분의 리만_합,Riemann_sum 그래프 그려서 알 수 있음 - 적분판정법,integral_test 비슷한 방법으로)
과 적분의 리만_합,Riemann_sum 그래프 그려서 알 수 있음 - 적분판정법,integral_test 비슷한 방법으로)
(강우석 2021-05-03 51m)
(강우석 2021-05-03 51m)
writing(see local)
mklink:
정수론,number_theory - 법,modulus / modulo .. 표현이? 암튼 정수,integer/자연수,natural_number 나눗셈,division에선 몫,quotient 말고도 나머지가 존재
나머지연산자 / modulo operator /
modulo operator /  remainder operator
remainder operator
나머지항,remainder_term - curr at 테일러_정리,Taylor_theorem .. curr see 테일러_정리#정의 Up: 나머지,remainder 항,term
테일러_정리#정의 Up: 나머지,remainder 항,term
나머지정리,remainder_theorem
{
다항식의 나머지정리
정수론,number_theory - 법,modulus / modulo .. 표현이? 암튼 정수,integer/자연수,natural_number 나눗셈,division에선 몫,quotient 말고도 나머지가 존재
나머지연산자 /
나머지항,remainder_term - curr at 테일러_정리,Taylor_theorem .. curr see
나머지정리,remainder_theorem
{
다항식의 나머지정리
어떤 다항식을 일차다항식  로 나눈 나머지는,
로 나눈 나머지는,
그 다항식의 변수에 를 대입하여 얻은 값과 같다는 정리.
를 대입하여 얻은 값과 같다는 정리.
그 다항식의 변수에
![[https]](/123/imgs/https.png) 수학백과: 나머지정리
수학백과: 나머지정리}
Chinese_remainder_theorem - writing
// PL의 정수나눗셈(정수나눗셈,integer_division or Euclidean_division - 정수,integer 나눗셈,division#s-1)에서 몫,quotient 말고 나머지를 구하는
나머지연산 - 연산,operation
나머지연산자 - 연산자,operator
{
pagename? mod/modulo/modulus/...중에 tbd
PL에 따라 % 혹은 MOD, mod
C++ std::modulus
https://en.cppreference.com/w/cpp/utility/functional/modulus
C++ std::remainder, std::remainderf, std::remainderl
https://en.cppreference.com/w/cpp/numeric/math/remainder
https://en.cppreference.com/w/cpp/utility/functional/modulus
C++ std::remainder, std::remainderf, std::remainderl
https://en.cppreference.com/w/cpp/numeric/math/remainder

