단순조화진동,simple_harmonic_oscillation

AKA 단조화진동, 조화단진동
줄여서 SHO (이건 -oscillator도 마찬가지인데..)

//이렇게 움직이는 물제는 단순조화진동자 simple harmonic oscillator? 단순조화진동자,simple_harmonic_oscillator Up: 조화진동자,harmonic_oscillator


tmp chk 항상이런건지 아닌지
{
일단 평형한/중간 ? 지점 .. 위치,position 이 있고
양 극단의 두 지점이 또 있고, 양극단 지점 사이를 왕복하며 이에 따라 변위,displacement가 바뀜,
보통 평형?중간? 지점에서 변위를 0으로 둠??

}


[edit]

설명

기준점(x=0)으로부터 변위 x가 시간 t에 대해
$x(t)=A\cos(\omega t+\delta)$
로 기술될 때 이 운동을 단조화진동이라 한다.

$A$ : 진폭,amplitude
$\omega t+\delta$ : 위상,phase
$\delta$ : t=0일때의 위상, 초기위상(initial phase) 또는 위상상수(phase constant)
위상상수,phase_constant

주기함수,periodic_function가 되려면,
$x(t+T)=x(t)$
$\cos(\omega(t+T)+\delta)=\cos(\omega t+\delta)$
만족하려면 $\omega T=2\pi$ 이어야 하므로 주기,period $T$ 는
$T=\frac{2\pi}{\omega}$
진동수,frequency $f$ 는
$f=\frac1{T}=\frac{\omega}{2\pi}$

$\omega$ : 각진동수,angular_frequency
$\omega=2\pi f=\frac{2\pi}{T}$

[edit]

원운동과 단조화 진동 사이의 대응관계


반지름 A로 원운동하는 물체의 x및 y축 상의 그림자 변위는 각각
$x=A\cos\theta,\quad y=A\sin\theta$
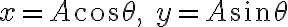
이다. 원운동의 각속도를 ω라 하면 x축에 대한 각변위 θ는 θ=ωt+δ로 주어진다. δ는 t=0에서 각변위이다. 따라서
$x=A\cos(\omega t+\delta),\quad y=A\sin(\omega t+\delta)$

원운동 단조화진동
A 반지름 진폭,amplitude
ω 각속도,angular_velocity 각진동수,angular_frequency
δ 초기 각변위 초기 위상 or 위상 상수
T 주기 주기,period
f 진동수 진동수,frequency

[edit]

Energy of the simple harmonic oscillator

Serway e6 p462에서

운동에너지,kinetic_energy는
$K=\frac12mv^2=\frac12m\omega^2A^2\sin^2(\omega t+\phi)$
elastic potential energy는
$U=\frac12kx^2=\frac12kA^2\cos^2(\omega t+\phi)$
둘을 더하면
$E=K+U=\frac12kA^2\left[\sin^2(\omega t+\phi)+\cos^2(\omega t+\phi)\right]$
따라서
$E=\frac12kA^2$

즉 진폭,amplitude의 제곱에 비례함을 알 수 있다.

[edit]

이정일 강의 보고 적은건데... CLEANUP DELME

$F=ma=-kx$
..
Define $\omega=\sqrt{k \over m}$
..
$v=\frac{\mathrm{d}x}{\mathrm{d}t}=\dot{x}$
$a=\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=\ddot{x}$

$x(t)=c_1e^{i\omega t}+c_2e^{-i\omega t}$
...
..삼각함수합성
$=\underbrace{c}_{\uparrow \atop {\rm amplitude}}\cos(\underbrace{\omega t-\delta}_{\uparrow \atop {\rm phase}})$
(진폭,amplitude and 위상,phase)

$x(t)=A\cos(\omega t-\delta)\;\Rightarrow\;\ddot{x}+\omega^2x=0$
$v(t)=\dot{x}(t)=-A\omega\sin(\omega t-\delta)$
$a(t)=\ddot{x}(t)=-A\omega^2\cos(\omega t-\delta)$

Initial conditions: x(0)=A and v(0)=0

$\omega={2\pi\over T}$
$T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}$