Difference between r1.12 and the current
@@ -1,3 +1,6 @@
'''de Moivre's formula, de Moivre's theorem, de Moivre's identity''' ([[공식,formula]] [[정리,theorem]] [[항등식,identity]] 모두에 해당)
## via Wikipedia (en)
$\cos(n\theta)+i\sin(n\theta)=(\cos\theta+i\sin\theta)^n$
@@ -5,9 +8,9 @@
관련: [[오일러_공식,Euler_formula]]see also [[복소수,complex_number#s-7.1]] - mv to here?
복소수의 거듭제곱과 관련?
복소수의 거듭제곱([[거듭제곱,power]] or [[멱,power]] or [[지수,exponentiation]])과 관련?
TBW 지수함수꼴 적을 것.
TBW Ggl:"드무아브르 지수함수꼴" 적을 것.
----
복소수 $z=e^{i\theta}=\cos\theta+i\sin\theta$ 를 $n$ 제곱 한다면,
@@ -16,7 +19,7 @@
드무아브르 공식에 $n=2$ 를 대입하면, 다음과 같이 실수부와 허수부를 써서 배각공식을 유도 가능.$(\cos^2\theta-\sin^2\theta)+(2\sin\theta\cos\theta)i=\cos(2\theta)+\sin(2\theta)i$
복소수에 관한 미니 지도서: http://paste.lisp.org/display/133628 (끝에 Common Lisp의 복소수 언급)
'복소수에 관한 미니 지도서': http://paste.lisp.org/display/133628 (끝에 Common_Lisp의 복소수 언급)
(Ivan Savov p221)
@@ -36,5 +39,5 @@
----
Up: [[공식,formula]]
[[정리,theorem]] [[항등식,identity]]
de Moivre's formula, de Moivre's theorem, de Moivre's identity (공식,formula 정리,theorem 항등식,identity 모두에 해당)
see also 복소수,complex_number#s-7.1 - mv to here?
복소수의 거듭제곱(거듭제곱,power or 멱,power or 지수,exponentiation)과 관련?
복소수의 거듭제곱(거듭제곱,power or 멱,power or 지수,exponentiation)과 관련?
복소수 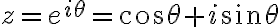 를
를  제곱 한다면,
제곱 한다면,
^n=z^n=(e^{i\theta})^n=e^{in\theta}=\cos n\theta+i\sin n\theta)
드무아브르 공식에 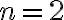 를 대입하면, 다음과 같이 실수부와 허수부를 써서 배각공식을 유도 가능.
를 대입하면, 다음과 같이 실수부와 허수부를 써서 배각공식을 유도 가능.
+(2\sin\theta\cos\theta)i=\cos(2\theta)+\sin(2\theta)i)
'복소수에 관한 미니 지도서': http://paste.lisp.org/display/133628 (끝에 Common_Lisp의 복소수 언급)
(Ivan Savov p221)
https://mathworld.wolfram.com/deMoivresIdentity.html - 드무아브르 항등식
{
여기선 지수형부터 먼저 설명하고 거기에 Euler formula를 대입. 원래 이런건가?
}=(e^{i\theta})^n)
따라서 Euler formula에 의해
+i\sin(n\theta)=(\cos\theta+i\sin\theta)^n)
쌍곡선함수,hyperbolic_function에서도 비슷한 항등식이 성립
^n = \operatorname{cosh}(nz)+\operatorname{sinh}(nz))
}
 De_Moivre's_formula
De_Moivre's_formula
 드무아브르의_공식
드무아브르의_공식
https://brilliant.org/wiki/de-moivres-theorem/
{
여기선 지수형부터 먼저 설명하고 거기에 Euler formula를 대입. 원래 이런건가?
https://brilliant.org/wiki/de-moivres-theorem/

