이거 identity = '항등성', identity_equation = '항등식' 이 more proper pagename 아닌가? see:
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Identity_(mathematics)
https://en.citizendium.org/wiki/Identity_(mathematics)
![[https]](/123/imgs/https.png) https://simple.wikipedia.org/wiki/Identity_(mathematics) - 이상 여기선 identity의 여러 뜻을 설명
https://simple.wikipedia.org/wiki/Identity_(mathematics) - 이상 여기선 identity의 여러 뜻을 설명
 Identity_(mathematics) - 여기선 identity_equation 을 본문에 설명하고 나머지 뜻은 첫줄에 'Not to be confused with'로 처리
Identity_(mathematics) - 여기선 identity_equation 을 본문에 설명하고 나머지 뜻은 첫줄에 'Not to be confused with'로 처리
2024-03-17
 identity보면 identity는 equation의 일종인 데 항상 성립하는 것. 그냥 _equation 안 붙여도 무방. 붙여도 무방하고.
identity보면 identity는 equation의 일종인 데 항상 성립하는 것. 그냥 _equation 안 붙여도 무방. 붙여도 무방하고.
2024-04-10 그냥 identity로 두는 게 낫겠다.
Sub:
오일러_항등식,Euler_identity
피타고라스 항등식 Pythagorean identity
베주_항등식,Bezout_identity
{
Bézout’s identity
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Identity_(mathematics)
https://en.citizendium.org/wiki/Identity_(mathematics)![[https]](/123/imgs/https.png) https://simple.wikipedia.org/wiki/Identity_(mathematics) - 이상 여기선 identity의 여러 뜻을 설명
https://simple.wikipedia.org/wiki/Identity_(mathematics) - 이상 여기선 identity의 여러 뜻을 설명2024-03-17
2024-04-10 그냥 identity로 두는 게 낫겠다.
오일러_항등식,Euler_identity
피타고라스 항등식 Pythagorean identity
베주_항등식,Bezout_identity
{
Bézout’s identity
Twins:
https://mathworld.wolfram.com/BezoutsIdentity.html
 베주_항등식
베주_항등식
 Bézout's_identity aka Bézout’s lemma
Bézout's_identity aka Bézout’s lemma
![[https]](/123/imgs/https.png) https://proofwiki.org/wiki/Bézout%27s_Lemma (Proof 1 : Euclidean_algorithm 을 반대로 하여 증명 가능)
https://proofwiki.org/wiki/Bézout%27s_Lemma (Proof 1 : Euclidean_algorithm 을 반대로 하여 증명 가능)
https://brilliant.org/wiki/bezouts-identity/
 베주 항등식
베주 항등식
 베주_항등식
베주_항등식
https://mathworld.wolfram.com/BezoutsIdentity.html
![[https]](/123/imgs/https.png) https://proofwiki.org/wiki/Bézout%27s_Lemma (Proof 1 : Euclidean_algorithm 을 반대로 하여 증명 가능)
https://proofwiki.org/wiki/Bézout%27s_Lemma (Proof 1 : Euclidean_algorithm 을 반대로 하여 증명 가능)https://brilliant.org/wiki/bezouts-identity/
야코비_항등식,Jacobi_identity - writing
polarization_identity - writing
Sophie_Germain_identity - writing
이것들을 항등성으로 묶어야할듯. 2021-12-27
Related:
항등행렬,identity_matrix → see 단위행렬,unit_matrix
항등함수,identity_function I ?? ... and identity_map
항등원,identity_element e ? - 이걸 줄여 'identity'로도 부름
항등함자? 상수함자? identity_functor
{
함자,functor
}
identity_type
{
,type ,type_theory에서 identity type = equality type
https://ncatlab.org/nlab/show/identity type
}
항등함수,identity_function I ?? ... and identity_map
항등원,identity_element e ? - 이걸 줄여 'identity'로도 부름
항등함자? 상수함자? identity_functor
{
함자,functor
}
identity_type
{
,type ,type_theory에서 identity type = equality type
https://ncatlab.org/nlab/show/identity type
}
2022-03-18
동치,equivalence
항등성, 항등 identity
상등 equality
동일, 같다(same), 같음, sameness
동치,equivalence
항등성, 항등 identity
상등 equality
동일, 같다(same), 같음, sameness
등호(=)
...이것들 관계를 아주 명확히 할 필요. 비교/disambig 필요. TBW ..... 써놓고 보니 동치,equivalence(writing)에 이미 써놓을 계획을 써놓음tmp from https://m.blog.naver.com/hafs_snu/221089512333
{
집합의 동일
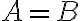
이것은 정의에 따라 A의 원소들이 전부 B의 원소이면서 동시에 vice versa 이면 A=B이다. (A⊆B ∧ A⊇B ⇒ A=B)
{
집합의 동일
집합의 cardinality의 동일
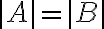
집합 A와 B가 동일한  cardinality를 가진다는 것은, A와 B 사이에 일대일대응관계one-to-one_correspondence(전단사,bijection)가 있다는 것.
cardinality를 가진다는 것은, A와 B 사이에 일대일대응관계one-to-one_correspondence(전단사,bijection)가 있다는 것.
}
}
너무 뻔한 항등식? del ok, 너무 당연하지만 일단 생각날때마다 나열... ¶
표기법만 다르게 한 것 포함
이것들은 solver나 CAS등을 만들 때 mathematical_expression의 simplifying·simplification/reduction에 쓰일 수 있을텐데.
이런것들을 대대적으로 정리/나열한 목록같은게 있을것같은데...
Q 이걸 항등식 페이지(여기)에 놔야 되나 아님 적당한 다른 page가 있나? 새 페이지를 만든다면 적당한 pagename? expression_simplification?
이것들은 solver나 CAS등을 만들 때 mathematical_expression의 simplifying·simplification/reduction에 쓰일 수 있을텐데.
이런것들을 대대적으로 정리/나열한 목록같은게 있을것같은데...
Q 이걸 항등식 페이지(여기)에 놔야 되나 아님 적당한 다른 page가 있나? 새 페이지를 만든다면 적당한 pagename? expression_simplification?
x+0=x. additive_identity
scalar_multiplication or scalar_multiple
{
무언가에 영,zero을 곱하면 항상 영.
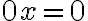
https://proofwiki.org/wiki/Real_Zero_is_Zero_Element - 이게 증명? (Munkres Topology)
}
{
무언가에 영,zero을 곱하면 항상 영.
https://proofwiki.org/wiki/Real_Zero_is_Zero_Element - 이게 증명? (Munkres Topology)
}
지수,exponentiation - exponent가 0이면 항상 1이 나오고,
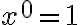
(다만 은 특수 취급해야 함. 보통 정의하지 않음. 이게 안전. 가끔 편의를(?) 위해 1로 두는 경우도 있는듯. (rel. 부정형,indeterminate_form?))
은 특수 취급해야 함. 보통 정의하지 않음. 이게 안전. 가끔 편의를(?) 위해 1로 두는 경우도 있는듯. (rel. 부정형,indeterminate_form?))
(다만
함수,function를 영 번 미분,differentiation한 것은 그 자체와 같고, 거기에 값을 대입한것도 당연히 같음
{
=f^{(0)}(x))
=f^{(0)}(a))
(via Taylor급수를 유도하는 과정에서 멱급수 ∑cn(x-a)n의 계수 c0, c1, ...의 값을 생각하려면)
}
{
(via Taylor급수를 유도하는 과정에서 멱급수 ∑cn(x-a)n의 계수 c0, c1, ...의 값을 생각하려면)
}
이런것들은 base_case {  base_case
base_case  base case Up: 경우,case } 와 느낌이 유사한데.
base case Up: 경우,case } 와 느낌이 유사한데.
rel.
reduction cancellation 공리,axiom 규칙,rule .....법칙,law? 제거,removal?
연역,deduction
rel.
reduction cancellation 공리,axiom 규칙,rule .....법칙,law? 제거,removal?
연역,deduction
논리,logic/수리논리,mathematical_logic의 law of identity
항등법칙,identity_law
{
law of identity
https://proofwiki.org/wiki/Law_of_Identity
Up: 논리,logic 항등성,identity 법칙,law
}
항등법칙,identity_law
{
law of identity
https://proofwiki.org/wiki/Law_of_Identity
Up: 논리,logic 항등성,identity 법칙,law
}
Up: 항등성,identity

