항상 수는 아니므로 코시 열이 더 정확한?
//from planetmath
거리공간,metric_space) 안의 수열,sequence
안의 수열,sequence 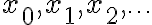 은 다음 조건을 만족하면 코시 수열(Cauchy sequence, fundamental sequence)이라 한다.
은 다음 조건을 만족하면 코시 수열(Cauchy sequence, fundamental sequence)이라 한다.
임의의 작은 양의 실수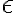 및 자연수
및 자연수 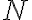 보다 큰 임의의
보다 큰 임의의 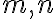 에 대해,
에 대해,
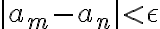
을 항상 만족하면 코쉬 수열이다.
정의에 의해 무한급수,infinite_series의 부분 합이 수렴한다면, 부분 합은 코쉬 수열이다.
거리공간,metric_space
모든 양의 실수 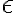 에 대해
에 대해 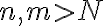 일 때마다
일 때마다 <\epsilon) 이 되는 자연수
이 되는 자연수 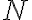 이 존재하면.
이 존재하면.
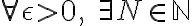 such that
such that <\epsilon)
//from https://ghebook.blogspot.com/2010/10/infinite-series.html 코쉬 수열임의의 작은 양의 실수
정의에 의해 무한급수,infinite_series의 부분 합이 수렴한다면, 부분 합은 코쉬 수열이다.
몇가지 명제. chk. from https://m.blog.naver.com/stforevery/40002809123
수렴,convergence - 가장 밀접한
완비공간,complete_space - 완비성,completeness - curr goto 최대최소정리,extreme_value_theorem,EVT, 실수,real_number, 유계,bounded
완비거리공간,complete_metric_space의 정의에는 코시 열을 사용함.
아르키메데스_성질,Archimedian_property - curr goto 해석학,analysis
- 모든 수렴하는 수열은 코시 수열이다.
- 모든 코시 수열은 유계,bounded이다.
- 코시수열의 모든 부분수열,subsequence은 코시수열이다.
- 주어진 코시수열이 수렴하는 부분수열을 가지면 그 코시수열은 수렴한다.
수렴,convergence - 가장 밀접한
완비공간,complete_space - 완비성,completeness - curr goto 최대최소정리,extreme_value_theorem,EVT, 실수,real_number, 유계,bounded
완비거리공간,complete_metric_space의 정의에는 코시 열을 사용함.
아르키메데스_성질,Archimedian_property - curr goto 해석학,analysis
tmp links en:
https://en.wikiversity.org/wiki/Cauchy_sequence
https://everything2.com/title/Cauchy sequence - a way of constructing the reals out of the rationals
https://en.wikiversity.org/wiki/Cauchy_sequence
https://everything2.com/title/Cauchy sequence - a way of constructing the reals out of the rationals
Twins:
https://foldoc.org/Cauchy sequence
https://mathworld.wolfram.com/CauchySequence.html
![[https]](/123/imgs/https.png) 수학백과: 코시 수열
수학백과: 코시 수열
 코시수열
코시수열
https://planetmath.org/cauchysequence
https://encyclopediaofmath.org/wiki/Cauchy_sequence
https://proofwiki.org/wiki/Definition:Cauchy_Sequence
https://ncatlab.org/nlab/show/Cauchy sequence
https://foldoc.org/Cauchy sequence
https://mathworld.wolfram.com/CauchySequence.html
![[https]](/123/imgs/https.png) 수학백과: 코시 수열
수학백과: 코시 수열https://planetmath.org/cauchysequence
https://encyclopediaofmath.org/wiki/Cauchy_sequence
https://proofwiki.org/wiki/Definition:Cauchy_Sequence
https://ncatlab.org/nlab/show/Cauchy sequence
AKA 기본수열 기본열 fundamental_sequence (수백)

